题目内容
在平面直角坐标系中,二次函数y=-x2+bx+c的图象与x轴交与点A(-1,0)B(4,0),且与y轴相交于C,在第一象限内抛物线上是否存在D,使得∠ADB=45°?若存在,求出点D坐标;若不存在,请说明理由.
考点:抛物线与x轴的交点
专题:
分析:易求得抛物线解析式,即可求得抛物线对称轴,在对称轴上取点O1 (
,
),设D(x,-x2+3x+4),易得AO1=
=DO1,整理即可求得x的值,即可解题.
| 3 |
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
解答:解:∵y=-x2+bx+c的图象与x轴交与点A(-1,0)B(4,0),
∴-1-b+c=0,-16+4b+c=0,
解得:b=3,c=4,
∴抛物线解析式为y=-x2+3x+4,
∴抛物线对称轴为x=
,
在对称轴上取点O1 (
,
),
设D(x,-x2+3x+4),
∵AO1=
=DO1,
∴(x-
)2+(-x2+3x+4-
)2=(
)2,
整理得:x4-6x3+7x2+6x-8=0,
∴(x4+7x2-8)+(-6x3+6x)=0,
(x2-1)(x2+8)-6x(x2-1)=0,
∴(x+1)(x-1)(x-2)(x-4)=0,
∴x1=-1,x2=1,x3=2,x4=4,
∴当x=1或2时,-x2+3x+4=6,
∴D1 (1,6),D2(2,6).
∴-1-b+c=0,-16+4b+c=0,
解得:b=3,c=4,
∴抛物线解析式为y=-x2+3x+4,
∴抛物线对称轴为x=
| 3 |
| 2 |
在对称轴上取点O1 (
| 3 |
| 2 |
| 5 |
| 2 |
设D(x,-x2+3x+4),
∵AO1=
5
| ||
| 2 |
∴(x-
| 3 |
| 2 |
| 5 |
| 2 |
5
| ||
| 2 |
整理得:x4-6x3+7x2+6x-8=0,
∴(x4+7x2-8)+(-6x3+6x)=0,
(x2-1)(x2+8)-6x(x2-1)=0,
∴(x+1)(x-1)(x-2)(x-4)=0,
∴x1=-1,x2=1,x3=2,x4=4,
∴当x=1或2时,-x2+3x+4=6,
∴D1 (1,6),D2(2,6).
点评:本题考查了二次函数解析式的求解,考查了一元二次方程的求解,本题中正确求得抛物线解析式是解题的关键.

练习册系列答案
相关题目
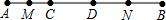 如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )
如图,C、D是线段AB上的两个点,CD=3cm,M是AC的中点,N是DB的中点,MN=5.4cm,那么线段AB的长等于( )| A、7.6cm | B、7.8cm |
| C、8cm | D、8.2cm |
 已知一次函数y=kx+b的图象如图所示,则下列语句正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列语句正确的是( )| A、当x<0时,y<0 |
| B、k+b<0 |
| C、函数值y随x的增大而减小 |
| D、kb>0 |
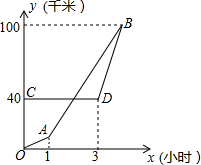 周末,甲从家出发前往与家相距100千米的旅游景点旅游,以10千米/时的速度步行1小时后,改骑自行车以30千米/时的速度继续向目的地出发,乙在甲前面40千米处,在甲出发3小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离y(千米)与甲出发的时间x(小时)之间的函数关系如图所示.
周末,甲从家出发前往与家相距100千米的旅游景点旅游,以10千米/时的速度步行1小时后,改骑自行车以30千米/时的速度继续向目的地出发,乙在甲前面40千米处,在甲出发3小时后开车追赶甲,两人同时到达目的地.设甲、乙两人离甲家的距离y(千米)与甲出发的时间x(小时)之间的函数关系如图所示. 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,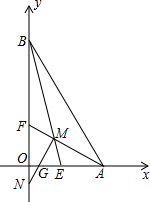 如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.
如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点. 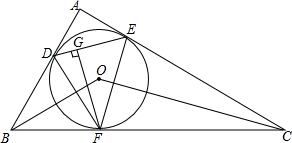 如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.
如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.