题目内容
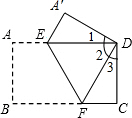 把一个长方形(对边平行且相等,每一个角均为直角)纸片按图进行折叠,使顶点B和D重合,折痕为EF.请问△A′ED与△CFD全等吗?若全等,请证明.
把一个长方形(对边平行且相等,每一个角均为直角)纸片按图进行折叠,使顶点B和D重合,折痕为EF.请问△A′ED与△CFD全等吗?若全等,请证明.考点:翻折变换(折叠问题)
专题:常规题型
分析:先根据矩形的性质得AB=CD,∠A=∠C=∠B=∠ADC=90°,再根据折叠的性质得∠A′=∠A=90°,∠A′DF=∠B=90°,A′D=AB,所以∠A′=∠C,A′D=CD,接着利用等角的余角相等得到∠1=∠3,然后根据“ASA”可判断△A′ED≌△CFD.
解答:解:△A′ED与△CFD全等.
证明过程如下:
∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=∠B=∠ADC=90°,
∵矩形ABCD沿EF折叠,使顶点B和D重合,
∴∠A′=∠A=90°,∠A′DF=∠B=90°,A′D=AB,
∴∠A′=∠C,A′D=CD,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
在△A′ED和△CFD中,
,
∴△A′ED≌△CFD.
证明过程如下:
∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=∠B=∠ADC=90°,
∵矩形ABCD沿EF折叠,使顶点B和D重合,
∴∠A′=∠A=90°,∠A′DF=∠B=90°,A′D=AB,
∴∠A′=∠C,A′D=CD,
∵∠1+∠2=90°,∠2+∠3=90°,
∴∠1=∠3,
在△A′ED和△CFD中,
|
∴△A′ED≌△CFD.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和三角形全等的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知一次函数y=kx+b的图象如图所示,则下列语句正确的是( )
已知一次函数y=kx+b的图象如图所示,则下列语句正确的是( )| A、当x<0时,y<0 |
| B、k+b<0 |
| C、函数值y随x的增大而减小 |
| D、kb>0 |
 如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )
如图,已知AB是⊙O的直径,CD切⊙O于点D,BE切⊙O于点B,交CD于点E,⊙O的半径为a,BC=na,则DE:EC=( )A、
| ||
B、
| ||
C、
| ||
D、
|
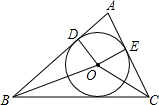 如图所示,⊙O是△ABC的内切圆,切AB、AC于点D、E.
如图所示,⊙O是△ABC的内切圆,切AB、AC于点D、E. 如图,在△ABC中,DE∥BC,
如图,在△ABC中,DE∥BC,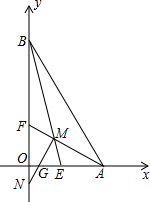 如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点.
如图,在平面直角坐标系中,AF、BE为角平分线,MN⊥AF交y轴于N点. 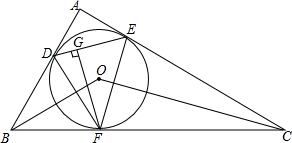 如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.
如图,△ABC的三边与其内切圆分别切于D、E、F三点,在△DEF中,作FG⊥DE,连结OB、OF、OC.求证:DG•CF=EG•BF.