题目内容
14. 利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?
利用一面长22米的墙围成一个形状为长方形的养鸡场.如图所示,养鸡场的一面靠墙其他三面用竹篱笆围成,并在一侧留有1米宽的门.现有长度为54米的竹篱笆.大李计划围成的养鸡场的长比宽多7米.小李计划围成的养鸡场的长比宽多4米,请你通过计算分析,谁的方案能够实现?此时养鸡场的面积是多少?
分析 由题意可知:墙可以当成一条边,那么长方形的长只有一个,宽有2个.等量关系为:2×宽+长=54,需注意长不能超过墙长22米.
解答 解:由大李的方案可以设宽为x米,则长为(x+7)米,由题意得
2x+(x+7)=54+1
解得:x=16
因此大李设计的长为x+7=23(米),而墙的长度只有22米,大李的设计方案不能够实现.
由小李的法可以设宽为y米,长为(y+4)米,
根据题意得2y+(y+4)=54+1
解得:y=17.
因此小李设计的长为y+4=21(米),而墙的长度有22米,显然小李的方案能够实现.
此时鸡场的面积为17×21=357(平方米).
点评 此题考查一元一次方程的实际运用,掌握长方形的周长计算方法是解决问题的关键.

练习册系列答案
相关题目
4.在下列各数-(+3),-22,(-2)2,(-1)2012,-|-5|中,负数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
2.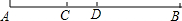 如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )
如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )
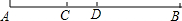 如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )
如图,已知线段AB=12cm,点C在线段AB上.且BC=2AC,D是线段AB的中点,则CD的长为( )| A. | 2cm | B. | 3cm | C. | 4cm | D. | 6cm |
19. 如图,从点O出发的四条射线.可以组成角的个数为( )
如图,从点O出发的四条射线.可以组成角的个数为( )
 如图,从点O出发的四条射线.可以组成角的个数为( )
如图,从点O出发的四条射线.可以组成角的个数为( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
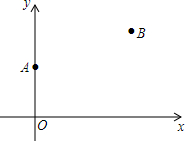 在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).
在一条公路的同侧有两个村庄A,B,若在公路上建一个加油站P,使得加油站到两个村庄的距离之和最小,即PA+PB最小.设公路为x轴,A点的坐标为(0,3),B点的坐标为(6,5).
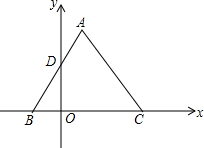 如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标.
如图是边长为4的等边△ABC,如果以BC所在直线为x轴,y轴经过AB的中点D点,请你求出点A、B、C的坐标.