题目内容
10.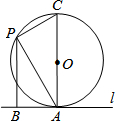 如图,直线l与半径为6的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于B点,连结AO并延长交⊙O于C点,连结PA、PC.①∠APC=90°度;②设PA=x,PB=y,则(x-y)的最大值是3.
如图,直线l与半径为6的⊙O相切于点A,P是⊙O上的一个动点(不与点A重合),过点P作PB⊥l于B点,连结AO并延长交⊙O于C点,连结PA、PC.①∠APC=90°度;②设PA=x,PB=y,则(x-y)的最大值是3.
分析 ①由圆周角定理可得,AC为直径,∠CPA=90°;
②得出△APC∽△PBA,利用$\frac{AP}{AC}=\frac{BP}{AP}$,得出x-y=x-$\frac{1}{12}$x2=-$\frac{1}{12}$x2+x=-$\frac{1}{12}$(x-6)2+3,所以x-y的最大值是3.
解答 解:①∵AC为直径,
∴∠CPA=90°,
故答案为:90°;
②∵AB是切线,
∴CA⊥AB,
∵PB⊥l,
∴AC∥PB,
∴∠CAP=∠APB,
∵∠CPA=90°,
∴△APC∽△PBA,
∴$\frac{AP}{AC}=\frac{BP}{AP}$,
∵PA=x,PB=y,半径为6,
∴$\frac{x}{12}$=$\frac{y}{x}$,
∴y=$\frac{1}{12}$x2,
∴x-y=x-$\frac{1}{12}$x2=-$\frac{1}{12}$x2+x=-$\frac{1}{12}$(x-6)2+3,
∴x-y的最大值是3.
故答案为3.
点评 此题考查了圆周角定理,切线的性质,平行线的性质,相似三角形的判定与性质,以及二次函数的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
5.已知等腰三角形的两条边长分别是7和3.则下列四个数可作为第三条边长的是( )
| A. | 3 | B. | 4 | C. | 7 | D. | 7或3 |
20.$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{\sqrt{2}}$ | D. | 2 |
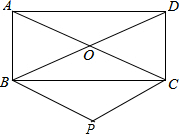 如图,在矩形ABCD中,对角线AC与DB相交于点O,CP∥DB,BP∥AC.
如图,在矩形ABCD中,对角线AC与DB相交于点O,CP∥DB,BP∥AC.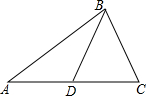 如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.
如图,BD是△ABC的中线,AB⊥BC,AD=2,AB=6,BC=3,则△ABD的面积是4.5.
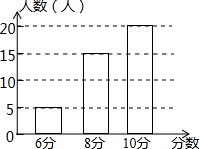 在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示,这次测试的平均分为8.75分.
在一次体育课上,体育老师对九年级一班的40名同学进行了立定跳远项目的测试,测试所得分数及相应的人数如图所示,这次测试的平均分为8.75分.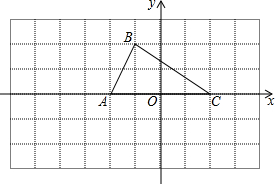 如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2).
如图,已知△ABC的三个顶点的坐标分别为A(-2,0),B(-1,2),C(2,0).请直接写出以A,B,C为顶点的平行四边形的第四个顶点D的坐标(3,2),(-5,2),(1,-2).