题目内容
14.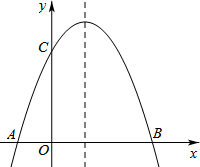 如图,已知抛物线y=ax2-2ax+3(a≠0)与x轴交于A、B两点,与y轴交于点C,且OB=3OA.
如图,已知抛物线y=ax2-2ax+3(a≠0)与x轴交于A、B两点,与y轴交于点C,且OB=3OA.(1)此抛物线的对称轴为直线x=1;并求出OA的长;
(2)求此抛物线的解析式;
(3)此二次函数x轴上方的图象上有一点E到A、B两点距离相等,求出△ABE的面积.
分析 (1)根据抛物线的对称轴为x=-$\frac{b}{2a}$,求出对称轴,根据根与系数的关系和OB=3OA求出OA的长;
(2)求出点A的坐标,根据坐标与函数的关系求出抛物线的解析式;
(3)根据题意确定点E的坐标求出△ABE的面积.
解答 解:(1)对称轴为直线x=-$\frac{-2a}{2a}$=1,
∴对称轴为直线x=1,
设OA=m,则OB=3m,
则-m+3m=2,
解得,m=1,
∴OA=1;
(2)∵OA=1,
∴点A(-1,0),
把点A(-1,0)代入y=ax2-2ax+3,
解得a=-1,
抛物线的解析式为:y=-x2+2x+3;
(3)二次函数图象上到A、B两点距离相等点E是抛物线的顶点,
$\frac{4ac-{b}^{2}}{4a}$=4,
则△ABE的面积为:$\frac{1}{2}$×4×4=8.
点评 本题考查的是抛物线与x轴的交点的求法,掌握二次函数的性质是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
则当y<10时,x的取值范围是-1<x<5.
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 10 | 5 | 2 | 1 | 2 | … |
2.英文单词“STRIVE”中,字母为中心对称图形的个数为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由.
如图,点A,B和点C,D分别在两个同心圆上,且AD=BC,∠AOB与∠COD相等?请说明你的理由. 如图,已知:BC为⊙O的直径,∠ADC=90°,AD与⊙O相切于F.
如图,已知:BC为⊙O的直径,∠ADC=90°,AD与⊙O相切于F. 如图,P是反比例函数y=$\frac{6}{x}$图象上一点,PA⊥x轴于点A,则△POA的面积S△POA=3.
如图,P是反比例函数y=$\frac{6}{x}$图象上一点,PA⊥x轴于点A,则△POA的面积S△POA=3.