题目内容
如图，四边形ABCD中，∠A=∠C=90°，则经过点A、B、D作⊙O，⊙O是否经过点C？考点：圆周角定理
专题：
分析：取弦BD的中点O，利用直角三角形斜边上的中线等于斜边的一半证得OA=OB=OC=OD后即可求证⊙O是否经过点C．
解答：
证明：⊙O经过点C；
连接BD，取弦BD的中点O，连接OC，OA，
∵∠A=∠C=90゜
∴DO，CO分别为Rt△ABD和Rt△BCD斜边上的中线，
∴OA=OB=OC=OD．
∴A、B、C、D四点在同一个圆上．
∴⊙O经过点C．
证明：⊙O经过点C；连接BD，取弦BD的中点O，连接OC，OA，
∵∠A=∠C=90゜
∴DO，CO分别为Rt△ABD和Rt△BCD斜边上的中线，
∴OA=OB=OC=OD．
∴A、B、C、D四点在同一个圆上．
∴⊙O经过点C．
点评：考查了圆的认识，求证几个点在同一个圆上就是证明这几个点到一个点的距离相等．
练习册系列答案
相关题目
下列等式中，从左边到右边的变形为分解因式的是（ ）
| A、12a2b=3a•4ab |
| B、（x+2）（x-2）=x2-4 |
| C、4x2-8x-1=4x（x-2）-1 |
| D、2ax-2ay=2a（x-y） |
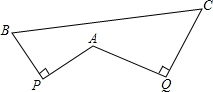如图，PA=PB且PA⊥PB，QA=QC且QA⊥QC．