题目内容
 如图,在一个直径为a+b的半圆中,挖去直径分别为a 和b的两个半圆,则图中阴影部分的面积为
如图,在一个直径为a+b的半圆中,挖去直径分别为a 和b的两个半圆,则图中阴影部分的面积为考点:整式的混合运算
专题:计算题
分析:大半圆面积减去两个小半圆面积求出阴影部分面积即可.
解答:解:根据题意得:
×π(
)2-
×π(
)2-
×π(
)2=
×(a2+2ab+b2-a2-b2)=
ab,
故答案为:
ab
| 1 |
| 2 |
| a+b |
| 2 |
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
| b |
| 2 |
| π |
| 8 |
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
关于x的一元二次方程kx2-x+1=0有两个不相等的实数根,则k的取值范围是( )
A、k<
| ||
B、k>
| ||
C、k<
| ||
D、k>
|
分式
没有意义,则x为( )
| x+1 |
| 3x-2 |
| A、-1 | ||
B、-1或
| ||
C、-1或
| ||
D、
|
下列等式中,从左边到右边的变形为分解因式的是( )
| A、12a2b=3a•4ab |
| B、(x+2)(x-2)=x2-4 |
| C、4x2-8x-1=4x(x-2)-1 |
| D、2ax-2ay=2a(x-y) |
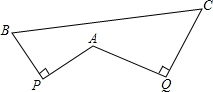 如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC.
如图,PA=PB且PA⊥PB,QA=QC且QA⊥QC.