题目内容
双曲线y=
与直线y=x-1有公共点,则k的取值范围是 .
| k |
| x |
考点:反比例函数与一次函数的交点问题
专题:计算题,判别式法
分析:整理为含x的一元二次方程,让根的判别式大于等于0列式求值即可.
解答:解:由题意得:x-1=
,
整理得x2-x-k=0,
∵双曲线y=
与直线y=x-1有公共点,
∴1+4k≥0,
解得k≥-
.
故答案为:k≥-
且k≠0.
| k |
| x |
整理得x2-x-k=0,
∵双曲线y=
| k |
| x |
∴1+4k≥0,
解得k≥-
| 1 |
| 4 |
故答案为:k≥-
| 1 |
| 4 |
点评:考查反比例函数和一次函数的交点问题;用到的知识点为:若2个函数有交点,整理所得的一元二次方程的根的判别式大于等于0.

练习册系列答案
相关题目
下列计算正确的是( )
| A、m3-m2=m | ||
B、
| ||
| C、(m+n)2=m2+n2 | ||
| D、(m3)2=m6 |
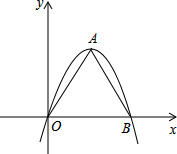 如图,抛物线解析式是y=-x2+bx(b>0),是否以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在请说明理由.
如图,抛物线解析式是y=-x2+bx(b>0),是否以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在请说明理由. 如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=6,BC=9,以A为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是
如图,梯形ABCD中,AD∥BC,∠C=90°,AB=AD=6,BC=9,以A为圆心在梯形内画出一个最大的扇形(图中阴影部分)的面积是