题目内容
12.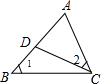 已知,如图,在△ABC中,点D在AB边上,连接CD,∠1=∠2.
已知,如图,在△ABC中,点D在AB边上,连接CD,∠1=∠2.(1)求证:△ACD∽△ABC;
(2)如果AD=2,BD=1,求AC的长.
分析 (1)根据相似三角形的判定定理即可得到结论;
(2)根据相似三角形的性质得到$\frac{AC}{AB}=\frac{AD}{AC}$,代入数据即可得到结果.
解答 (1)证明:∵∠1=∠2,∠A=∠A,
∴△ACD∽△ABC;
(2)解:∵△ACD∽△ABC,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AB•AD,
∵AD=2,BD=1,
∴AB=3,
∴AC=$\sqrt{6}$.
点评 本题考查了相似三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
2.一个不透明的袋子中装有5个红球,3个黄球,2个蓝球,这些球除了颜色外都相同,从中任意摸出一个球,则摸出蓝球的可能性为( )
| A. | 0.5 | B. | 0.4 | C. | 0.3 | D. | 0.2 |
3.已知点P(a,b)满足ab<0,a-b>0,则点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.下列事件中是必然事件的是( )
| A. | 打开电视机,正在播无棣新闻 | |
| B. | 今年春节,我们县的天气一定是晴天 | |
| C. | “大衣哥”朱之文一定能上2016年春节联欢晚会 | |
| D. | 从一个只装有红球的箱子里摸出一个球,摸出的球是红球 |