题目内容
8. 如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM为2.
如图,正六边形ABCDEF内接于圆O,半径为4,则这个正六边形的边心距OM为2.
分析 由正六边形的性质得出∠AOM=60°,OA=4,求出∠OAM=30°,由含30°角的直角三角形的性质得出OM=$\frac{1}{2}$OA=2即可.
解答 解:∵六边形ABCDEF是正六边形,OM⊥AC,
∴∠AOM=60°,∠OMA=90°,OA=4,
∴∠OAM=30°,
∴OM=$\frac{1}{2}$OA=2,
即这个正三角形的边心距OM为2;
故答案为:2.
点评 本题考查了正六边形的性质、正三角形的性质、含30°角的直角三角形的性质;熟练掌握正六边形的性质,由含30°角的直角三角形的性质求出OM是解决问题的关键.

练习册系列答案
相关题目
19.已知二次三项式x2-4x+m有一个因式是x+3,求另一个因式以及m的值时,可以设另一个因式为x+n,则x2-4x+m=(x+3)(x+n).
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
即x2-4x+m=x2+(n+3)x+3n.
∴$\left\{\begin{array}{l}{n+3=-4}\\{m=3n}\end{array}\right.$解得,n=-7,m=-21,
∴另一个因式为x-7,m的值为-21.
类似地,二次三项式2x2+3x-k有一个因式是2x-5,则它的另一个因式以及k的值为( )
| A. | x-1,5 | B. | x+4,20 | C. | x$+\frac{3}{2}$,$\frac{15}{2}$ | D. | x+4,-4 |
13. 如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
 如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )
如图所示,在正方形网格中,图②是由图①经过旋转变换得到的,其旋转中心是点( )| A. | A点 | B. | B点 | C. | C点 | D. | 无法确定 |

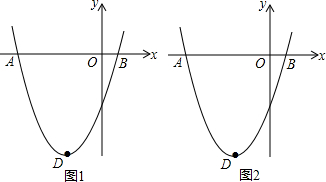
 如图,AB∥CD,且AO=CO.求证:AB=CD.
如图,AB∥CD,且AO=CO.求证:AB=CD.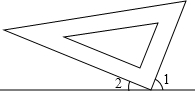 三角板的直角顶点在直线l上,若∠1=40°15′,则∠2的度数是49°45′.
三角板的直角顶点在直线l上,若∠1=40°15′,则∠2的度数是49°45′.