题目内容
17.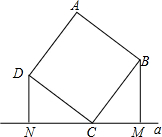 如图,正方形ABCD的顶点C在直线a上,且点B、D到a的距离BM、DN分别是1,2,则这个正方形的边长是$\sqrt{5}$.
如图,正方形ABCD的顶点C在直线a上,且点B、D到a的距离BM、DN分别是1,2,则这个正方形的边长是$\sqrt{5}$.
分析 先证明△BMC≌△NCD,再用勾股定理即可求解.
解答 解:∵∠MBC+∠BCM=∠NCD+∠BCM=90°
∴∠MBC=∠NCD
在△BMC和△NCD中
$\left\{\begin{array}{l}{∠MBC=∠NCD}\\{∠BMC=∠CND=90°}\\{BC=CD}\end{array}\right.$
∴△BMC≌△NCD
∴MC=ND=2
∴BC=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$.
故答案为:$\sqrt{5}$.
点评 本题考查了三角形全等的判定和勾股定理以及正方形的性质的应用,熟练的运用全等三角形的判定是解决问题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
8.下列式子正确的是( )
| A. | $\sqrt{16}$=±4 | B. | $\sqrt{(-\frac{1}{3})^{2}}$=$\frac{1}{3}$ | C. | $\sqrt{-1\frac{7}{9}}$=-1$\frac{1}{3}$ | D. | $\root{3}{-9}$=-3 |
12.某中学随机抽查了50名学生,了解他们一周的课外阅读时间,结果如表所示:
则这50名学生一周的平均课外阅读时间是5.3小时.
| 时间(小时) | 4 | 5 | 6 | 7 |
| 人数 | 10 | 20 | 15 | 5 |
6. 如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )
如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )
 如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )
如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
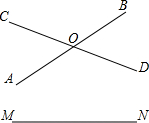 如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,方法是分别作∠AOD及∠AOC的平分线OE与OF,这样的点至少有1个,最多有2个.
如图,已知相交直线AB和CD及另一直线MN,如果要在MN上找出与AB,CD距离相等的点,方法是分别作∠AOD及∠AOC的平分线OE与OF,这样的点至少有1个,最多有2个.