题目内容
6. 如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )
如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )| A. | 10 | B. | 8 | C. | 6 | D. | 4 |
分析 延长BD交AC于点E,则可知△ABE为等腰三角形,则S△ABD=S△ADE,S△BDC=S△CDE,可得出S△ADC=$\frac{1}{2}$S△ABC.
解答 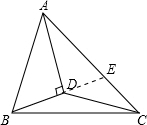 解:如图,延长BD交AC于点E,
解:如图,延长BD交AC于点E,
∵AD平分∠BAE,AD⊥BD,
∴∠BAD=∠EAD,∠ADB=∠ADE,
在△ABD和△AED中,
$\left\{\begin{array}{l}{∠BAD=∠EAD}\\{AD=AD}\\{∠BDA=∠EDA}\end{array}\right.$,
∴△ABD≌△AED(ASA),
∴BD=DE,
∴S△ABD=S△ADE,S△BDC=S△CDE,
∴S△ABD+S△BDC=S△ADE+S△CDE=S△ADC,
∴S△ADC═$\frac{1}{2}$S△ABC=$\frac{1}{2}$×12=6,
故选C.
点评 本题主要考查等腰三角形的判定和性质,由BD=DE得到S△ABD=S△ADE,S△BDC=S△CDE是解题的关键.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
18. 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
 如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )
如图,C点在线段AB上,点D是AC的中点,若CD=4cm,AB=13cm,则BC的长为( )| A. | 4cm | B. | 5cm | C. | 8cm | D. | 9cm |
15.下列各式中,与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{6}$ | B. | $\sqrt{15}$ | C. | $\sqrt{18}$ | D. | $\sqrt{\frac{1}{12}}$ |
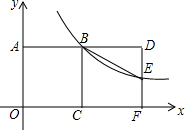 如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE.
如图,边长为2的正方形ABCO的顶点C、A分别在x轴、y轴上,函数y=$\frac{k}{x}$(x>0)的图象经过点B,把正方形ABCO沿BC翻折得到正方形BCFD,DF交这个函数的图象于点E,连结BE.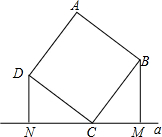 如图,正方形ABCD的顶点C在直线a上,且点B、D到a的距离BM、DN分别是1,2,则这个正方形的边长是$\sqrt{5}$.
如图,正方形ABCD的顶点C在直线a上,且点B、D到a的距离BM、DN分别是1,2,则这个正方形的边长是$\sqrt{5}$.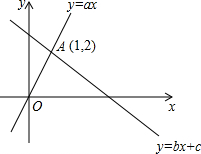 如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为x>1.
如图,函数y=ax和y=bx+c的图象相交于点A(1,2),则不等式ax>bx+c的解集为x>1. 如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.
如图,抛物线y=-x2-2x+3与x轴交于A、B两点,与y轴交于点C,M为抛物线的顶点,点P为x轴负半轴上一点,PC交AM于E,若AE=CE,求点P的坐标.