题目内容
2.若关于x的方程$\frac{x+m}{x-3}+\frac{3m}{3-x}$=3的解为非负数,则m的取值范围是m≤$\frac{9}{2}$且m≠$\frac{3}{2}$.分析 分式方程去分母转化为整式方程,由分式方程的解为非负数,确定出m的范围即可.
解答 解:去分母得:x+m-3m=3x-9,
解得:x=$\frac{9-2m}{2}$,
由分式方程的解为非负数,得到$\frac{9-2m}{2}$≥0且$\frac{9-2m}{2}$≠3,
解得:m≤$\frac{9}{2}$且m≠$\frac{3}{2}$,
故答案为:m≤$\frac{9}{2}$且m≠$\frac{3}{2}$
点评 此题考查了分式方程的解,以及解一元一次不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.在实数-3,2,0,-1中,最小的数是( )
| A. | -3 | B. | 2 | C. | 0 | D. | -1 |
10.下列事件中是必然事件的是( )
| A. | 从一个装满黑球的布袋中摸出一个球是黑球 | |
| B. | 抛掷1枚普通硬币得到正面朝上 | |
| C. | 抛掷1颗正方体骰子得到的点数是偶数 | |
| D. | 抛掷1个普通图钉一定是针尖向下 |
12.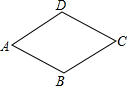 如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )
如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )
 如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )
如图,广场中心的菱形花坛ABCD的周长是40米,∠A=60°,则A,C两点之间的距离为( )| A. | 5米 | B. | 5$\sqrt{3}$米 | C. | 10米 | D. | 10$\sqrt{3}$米 |
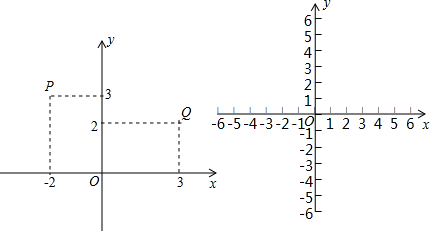
 如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{12}{x}$(x>0)的图象交于A(m,6),B(n,3)两点.
 如图,△ABC是直角三角形,∠ACB=90°.
如图,△ABC是直角三角形,∠ACB=90°.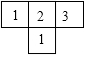 由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )
由7个大小相同的小正方体组合成一个几何体.其俯视图如图所示,其中正方形中的数字表示该位置放置的小正方体的个数,则该几何体的左视图为( )