题目内容
6.解方程组:$\left\{\begin{array}{l}y=2x-7\\ x+y+z=1\\ 3x-z=4.\end{array}\right.$.分析 利用代入消元法先消去y,再利用加减消元法消去未知数z,即可求得x的值,由此代入即可分别求得x、y、z的值.
解答 解:$\left\{\begin{array}{l}{y=2x-7\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;①}\\{x+y+z=1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;②}\\{3x-z=4\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;③}\end{array}\right.$;
把①代入②可得:x+2x-7+z=1,
整理可得:3x+z=8,④;
③+④可得:6x=12,则x=2,
把x=2代入①,可得y=-3;
把x=2,y=-3代入②,可得z=2,
所以这个方程组的解是:$\left\{\begin{array}{l}x=2\\ y=-3\\ z=2.\end{array}\right.$.
点评 此题考查了利用代入消元法和加减消元法解三元一次方程组的灵活应用.

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
20.如图是两户居民家庭在同一段时间内各项支出的统计图,根据统计图,下列对两户居民教育支出金额作出的判断中,正确的是( )
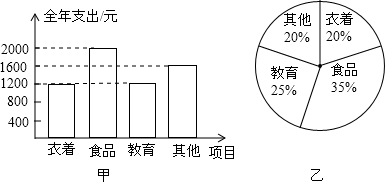

| A. | 甲户比乙户大 | B. | 乙户比甲户大 | ||
| C. | 甲、乙两户一样大 | D. | 无法确定哪一户大 |
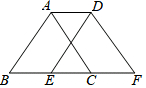 如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm.
如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm. 计算下面圆锥体的体积.(单位:厘米)
计算下面圆锥体的体积.(单位:厘米)