题目内容
 如图,在△ABC中,AC=2,∠A=45°,tanB=
如图,在△ABC中,AC=2,∠A=45°,tanB=| 1 |
| 2 |
考点:解直角三角形
专题:
分析:过点C作CD⊥AB于D,利用∠A的正弦值求出CD,再根据∠B的正切值求出BD,利用勾股定理列式求出BC的长.
解答:
 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,
∵AC=2,∠A=45°,
∴CD=AC•sin∠A=2•sin45°=2×
=
,
∵tanB=
,
∴BD=
=
=2
,
∴BC=
=
=
.
故答案为
.
 解:如图,过点C作CD⊥AB于D,
解:如图,过点C作CD⊥AB于D,∵AC=2,∠A=45°,
∴CD=AC•sin∠A=2•sin45°=2×
| ||
| 2 |
| 2 |
∵tanB=
| 1 |
| 2 |
∴BD=
| CD |
| tanB |
| ||
|
| 2 |
∴BC=
| CD2+BD2 |
(
|
| 10 |
故答案为
| 10 |
点评:本题考查了解直角三角形,作辅助线构造出两个直角三角形是解题的关键.

练习册系列答案
相关题目
对于分式
,永远成立的是( )
| 1 |
| x-1 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若反比例函数y=
图象在各个象限内y随着x的增大而增大,则m满足( )
| m+2 |
| x |
| A、m<-2 | B、m>-2 |
| C、m<2 | D、m>2 |
下列各式中,分式的个数有( )
(1)
;(2)
;(3)
;(4)
;(5)
;(6)
.
(1)
| 1 |
| x |
| x |
| 3 |
| y |
| 2x2 |
| m-n |
| m+n |
| -x |
| 5 |
| a |
| b |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列给出的方程中,不是二元一次方程的是( )
| A、2x-2y=3 | ||
B、
| ||
C、
| ||
D、
|
 如图,在平面直角坐标系中,第一象限内的双曲线y=
如图,在平面直角坐标系中,第一象限内的双曲线y=
 用小立方体搭成的几何体的主视图和俯视图如图,问:这样的几何体是否只有一种?它最少需多少个立方体?它最多需多少个立方体?请画出最多与最少时的左视图.
用小立方体搭成的几何体的主视图和俯视图如图,问:这样的几何体是否只有一种?它最少需多少个立方体?它最多需多少个立方体?请画出最多与最少时的左视图.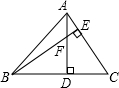 已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.
已知:如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,且AF=DF,∠EAD=30°.求证:BF=4EF.