题目内容
19.解方程:(1)$\frac{4+x}{x-1}-5=\frac{2x}{x-1}$.
(2)$\frac{1}{x-3}+2=\frac{x-4}{3-x}$.
分析 (1)两边乘(x-1)化为整式方程求解,注意必须检验.
(2)两边乘(x-3)化为整式方程求解,注意必须检验.
解答 解:(1)两边乘(x-1)得4+x-5(x-1)=2x,
4+x-5x+5=2x,
6x=9,
∴x=$\frac{3}{2}$,
检验:当x=$\frac{3}{2}$时,x-1≠0,
∴x=$\frac{3}{2}$是分式方程是根.
(2)两边乘(x-3)得1+2(x-3)=-(x-4),
1+2x-6=-x+4,
3x=9,
∴x=3,
检验:当x=3时,x-3=0,
∴x=3是增根,原分式方程无解.
点评 本题考查解分式方程,解题的关键是掌握解方程的步骤,注意解分式方程必须检验,属于中考基础题,常考题型.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
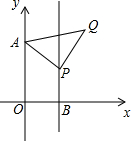 如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$.
如图,已知在平面直角坐标系xOy中,O为坐标原点,A(0,5),B(3,0),过点B作直线l∥y轴,点P(3,b)是直线l上的一个动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ=90°,当点P在直线l上运动时,点Q也随时之运动,问:当b=$\frac{23}{7}$时,AQ+BQ的值最小为$\sqrt{130}$.