题目内容
9．不等式组$\left\{\begin{array}{l}{3x＜2x+4}\\{\frac{3-x}{3}≥2}\end{array}\right.$的解集，在数轴上表示正确的是（ ）| A． |  | B． |  | ||
| C． |  | D． |  |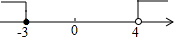
分析 解出不等式组的解集，即可得到哪个选项是正确的，本题得以解决．
解答 解：$\left\{\begin{array}{l}{3x＜2x+4}&{①}\\{\frac{3-x}{3}≥2}&{②}\end{array}\right.$
由①，得x＜4，
由②，得x≤-3，
由①②得，原不等式组的解集是x≤-3；
故选A．
点评 本题考查解一元一次不等式组、在数轴上表示不等式的解集，解题的关键是明确解一元一次不等式组的方法．
练习册系列答案
名校课堂系列答案
相关题目
20．计算（-2）0+9÷（-3）的结果是（ ）
| A． | -1 | B． | -2 | C． | -3 | D． | -4 |
如图，已知二次函数y1=ax2+bx过（-2，4），（-4，4）两点．
14．下列实数中，有理数是（ ）
| A． | $\sqrt{8}$ | B． | $\root{3}{4}$ | C． | $\frac{π}{2}$ | D． | 0.101001001 |
如图，在平面直角坐标系中，菱形OABC的面积为12，点B在y轴上，点C在反比例函数y=$\frac{k}{x}$的图象上，则k的值为-6．
18．在实数-$\frac{1}{3}$，-2，0，$\sqrt{3}$中，最小的实数是（ ）
| A． | -2 | B． | 0 | C． | -$\frac{1}{3}$ | D． | $\sqrt{3}$ |