题目内容
12.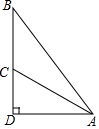 如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,求旗杆BC的高度.
如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,坡顶有一旗杆BC,旗杆顶端B点与A点有一条彩带相连,若AB=10米,求旗杆BC的高度.
分析 直接利用已知结合勾股定理得出DC,AD的长,再利用勾股定理得出BC的长.
解答 解:∵斜面AC的坡度(CD与AD的比)为1:2,AC=3$\sqrt{5}$米,
∴设DC=x,则AD=2x,
故在Rt△ADC中,
x2+(2x)2=(3$\sqrt{5}$)2,
解得:x=3,
故DC=3m,AD=6m,
∵AB=10m,
故在Rt△ADB中,
(BC+3)2+62=102,
解得:BC=5,
答:旗杆BC的高度为5m.
点评 此题主要考查了解直角三角形的应用,正确得出DC的长是解题关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
3.如图是若干个边长均为1cm的正方形组成的网格,正方形的顶点也叫格点,如果一个多边形的顶点全是格点,这个多边形叫格点多边形,这样的多边形的面积计算起来很方便,只要数一下多边形各边上格点数的总和及这个多边形内的格点数就可以用公式计算,现在我们就来探究这个公式.
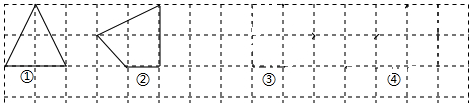
探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
探究三 当格点多边形内只有三个格点并且各边上格点数的总和为n个时,格点多边形的面积S=$\frac{1}{2}$n+2(用含n的代数式表示)
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)

探究一 格点多边形内只有一个格点. 请根据图形填写下列表格
探究二 格点多边形内只有两个格点
请在网格中画出符合条件的两个格点多边形,根据你画出的图形,完善表格中相应的内容.
| 图形编号 | 多边形内格点数/个 | 多边形各边上格点数的总和/个 | 多边形的面积/cm2 |
| ① | 1 | 4 | 2 |
| ② | 1 | 5 | $\frac{5}{2}$ |
| ③ | 2 | 10 | 6 |
| ④ | 2 | 4 | 3 |
猜想 当格点多边形内有m个格点并且各边上格点总数的和为n个时,格点多边形的面积S=$\frac{1}{2}$n+m-1(用含m,n的代数式表示)
20.已知两个相似三角形的面积之比是4:9,那么这两个三角形周长的比是( )
| A. | 4:9 | B. | 9:4 | C. | 16:81 | D. | 2:3 |
2. 一个空心的圆柱如图,那么它的左视图是( )
一个空心的圆柱如图,那么它的左视图是( )
 一个空心的圆柱如图,那么它的左视图是( )
一个空心的圆柱如图,那么它的左视图是( )| A. |  | B. |  | C. |  | D. |  |
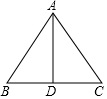 (1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么?
(1)如图,AD是△ABC的中线,△ABC与△ABD的面积有怎样的数量关系?为什么?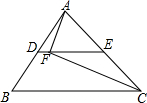 如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为14.
如图,在△ABC中,D,E分别是AB,AC的中点,AC=12,F是DE上一点,连接AF,CF,DF=1.若∠AFC=90°,则BC的长度为14.