题目内容
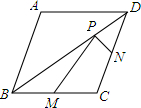 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).
已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上的动点(不含B、D).(1)证明无论动点P在何处,四边形PMCN的面积总是固定值,这个固定值是多少?
(2)试探究动点P在何处时,四边形PMCN的周长最小,最小值是多少?
考点:菱形的性质,轴对称-最短路线问题
专题:
分析:(1)利用中位线的性质以及平行线的性质得出△PMN的面积=△BMN的面积=△CMN的面积,进而求出即可;
(2)利用轴对称的性质结合菱形的性质得出MP+NP=QP+NP=QN=5,求出即可.
(2)利用轴对称的性质结合菱形的性质得出MP+NP=QP+NP=QN=5,求出即可.
解答:解:(1)如图所示:
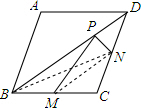
∵M、N分别是边BC、CD的中点,∴MN∥BD.
∴△PMN的面积=△BMN的面积=△CMN的面积,
∴四边形PMCN的面积=
菱形ABCD的面积=6;
(2)如图所示:
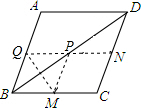
作M关于BD的对称点Q,连接NQ交BD于P,连接MP,此时MP+NP的值最小,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CO=AC=3,BO=BD=4,
在Rt△BOC中,由勾股定理得:BC=5,即NQ=5,
∴MP+NP=QP+NP=QN=5,
∴四边形PMCN周长最小值是10.

∵M、N分别是边BC、CD的中点,∴MN∥BD.
∴△PMN的面积=△BMN的面积=△CMN的面积,
∴四边形PMCN的面积=
| 1 |
| 4 |
(2)如图所示:

作M关于BD的对称点Q,连接NQ交BD于P,连接MP,此时MP+NP的值最小,
∵四边形ABCD是菱形,
∴AC⊥BD,∠QBP=∠MBP,即Q在AB上,
∵MQ⊥BD,
∴AC∥MQ,
∵M为BC中点,
∴Q为AB中点,
∵N为CD中点,四边形ABCD是菱形,
∴BQ∥CD,BQ=CN,
∴四边形BQNC是平行四边形,
∴NQ=BC,
∵四边形ABCD是菱形,
∴CO=AC=3,BO=BD=4,
在Rt△BOC中,由勾股定理得:BC=5,即NQ=5,
∴MP+NP=QP+NP=QN=5,
∴四边形PMCN周长最小值是10.
点评:此题主要考查了菱形的性质以及轴对称求最短路线,正确利用对称性得出P点位置是解题关键.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
化简
的结果为( )
| (tan60°-1)2 |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
 有理数a,b在数轴上的位置如图所示,那么下列式子中不一定成立的是( )
有理数a,b在数轴上的位置如图所示,那么下列式子中不一定成立的是( )| A、a>b | ||
| B、b-a<0 | ||
C、
| ||
| D、|a|≥|b| |
 如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )
如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )| A、120° | B、150° |
| C、75° | D、60° |
下列事件中,为必然事件的是( )
| A、某射击运动员射击一次,命中靶心 |
| B、经过城市中某一有交通信号的路口,遇到红灯 |
| C、抛掷一枚硬币,正面向上 |
| D、掷一枚骰子,点数大于0 |
 如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问:
如图,点P是菱形ABCD的对角线BD上一点,连结CP并延长,交AD于E,交BA的延长线于点F.试问: