Question

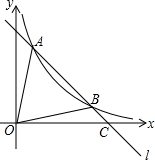如图，直线l与反比例函数y=

k

x

在第一象限内的图象交于A、B两点，且与x轴的正半轴交于C点．若AB=2BC，△OAB的面积为8，则k的值为（　　）

• A、6
• B、9
• C、12
• D、18

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：作AD⊥x轴于D，BE⊥x轴于E，先证明△CBE∽△CAD，利用相似比得到AD=3BE，设B（t，

k

t

），利用反比例函数图象上点的坐标特征得到A点坐标为（

1

3

t，

3k

t

），根据反比例函数的比例系数的几何意义得S_△AOD=S_△BOE，由于S_△AOD+S_梯形ABED=S_△AOB+S_△BOE，所以S_△AOB=S_梯形ABED，然后利用梯形的面积公式计算即可求得．

解答：解：作AD⊥x轴于D，BE⊥x轴于E，如图，
∵BE∥AD，
∴△CBE∽△CAD，
∴

BE

AD

=

CB

CA

，
∵AB=2BC，
∴CB：CA=1：3，
∴

BE

AD

=

CB

CA

=

1

3

，
∴AD=3BE，
设B（t，

k

t

），则A点坐标为（

1

3

t，

3k

t

），
∵S_△AOD+S_梯形ABED=S_△AOB+S_△BOE，
而S_△AOD=S_△BOE，=

1

2

k，
∴S_△AOB=S_梯形ABED=

1

2

（

k

t

+

3k

t

）•（t-

1

3

t）=8，
解得，k=6．
故选A．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数图象的交点坐标满足两函数解析式．也考查了相似三角形的判定与性质．