题目内容
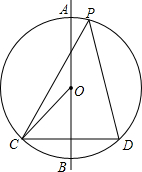 在⊙O中,AB是直径,CD是弦,AB⊥CD.
在⊙O中,AB是直径,CD是弦,AB⊥CD.(1)P是优弧CAD上一点(不与C、D重合),求证:∠CPD=∠COB;
(2)点P′在劣弧CD上(不与C、D重合)时,∠CP′D与∠CPB有什么关系?请说明你的结论.
考点:圆周角定理,垂径定理
专题:
分析:(1)根据垂径定理知,
=2
,由圆周角定理知,
的度数等于∠BOC的度数,
的度数等于∠CPD的2倍可得出结论;
(2)根据圆内接四边形的对角互补知,∠CP′D=180°-∠CPD,而∠CPD=∠COB,故∠CP′D+∠COB=180°.
 |
| CD |
 |
| BC |
 |
| BC |
 |
| AD |
(2)根据圆内接四边形的对角互补知,∠CP′D=180°-∠CPD,而∠CPD=∠COB,故∠CP′D+∠COB=180°.
解答: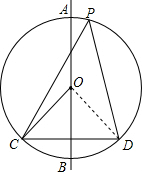 (1)证明:如图所示,连接OD.
(1)证明:如图所示,连接OD.
∵AB是直径,AB⊥CD,
∴
=
,
∴∠COB=∠DOB=
∠COD.
又∵∠CPD=
∠COD,
∴∠CPD=∠COB;
(2)解:∠CP'D与∠COB的数量关系是∠CP'D+∠COB=180°.
理由:∵∠CPD=
∠COD,∠CP'D=
(360°-∠COD)=180°-
∠COD,
∴∠CPD+∠CP'D=180°
由(1)知,∠CPD=∠COB,
∴∠CP'D+∠COB=180°.
 (1)证明:如图所示,连接OD.
(1)证明:如图所示,连接OD.∵AB是直径,AB⊥CD,
∴
 |
| BC |
 |
| BD |
∴∠COB=∠DOB=
| 1 |
| 2 |
又∵∠CPD=
| 1 |
| 2 |
∴∠CPD=∠COB;
(2)解:∠CP'D与∠COB的数量关系是∠CP'D+∠COB=180°.
理由:∵∠CPD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CPD+∠CP'D=180°
由(1)知,∠CPD=∠COB,
∴∠CP'D+∠COB=180°.
点评:本题考查的是圆周角定理,根据题意作出辅助线,构造出圆心角是解答此题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
化简
的结果为( )
| (tan60°-1)2 |
A、1-
| ||||
B、1-
| ||||
C、
| ||||
D、
|
 如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )
如图,量角器的直径与含30°角的直角三角形ABC的斜边AB重合,射线CP从CA处出发沿顺时针方向以每秒2度的速度旋转,CP与量角器的半圆弧交于点E,当第30秒时,点E在量角器上对应的读数是( )| A、120° | B、150° |
| C、75° | D、60° |
在同一平面内,连接一个定点和圆上的任意一点的线段中,最短为4cm,最长为9cm,则该圆的半径是( )
| A、2.5cm或6.5cm |
| B、2.5cm |
| C、6.5cm |
| D、5cm或13cm |
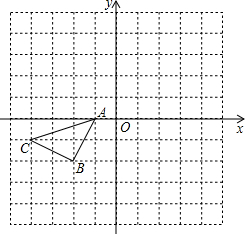 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题: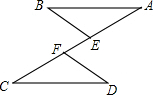 如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是
如图,已知AB∥CD,AE=CF,则下列条件:①AB=CD;②BE∥DF;③∠B=∠D;④BE=DF.其中不一定能使△ABE≌△CDF的是