题目内容
1.$\sqrt{2}$-1的倒数为( )| A. | $\sqrt{2}$-1 | B. | 1-$\sqrt{2}$ | C. | $\sqrt{2}$+1 | D. | -$\sqrt{2}$-1 |
分析 首先根据互为倒数的两个数的乘积是1,用1除以$\sqrt{2}-1$,求出它的倒数是多少;然后根据分母有理化的方法,把$\frac{1}{\sqrt{2}-1}$分母有理化即可.
解答 解:∵$1÷({\sqrt{2}-1})=\frac{1}{{\sqrt{2}-1}}=\frac{{\sqrt{2}+1}}{{({\sqrt{2}-1})({\sqrt{2}+1})}}=\sqrt{2}+1$,
∴$\sqrt{2}-1$的倒数为:$\sqrt{2}+1$.
故选:C.
点评 (1)此题主要考查了分母有理化的含义,以及分母有理化的方法,要熟练掌握.
(2)此题还考查了两个数互为倒数的含义和性质的应用,要熟练掌握,解答此题的关键是要明确:互为倒数的两个数的乘积是1.

练习册系列答案
相关题目
11.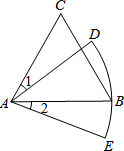 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
 如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )
如图,△ABC是等边三角形,AC=6,以点A为圆心,AB长为半径画弧DE,若∠1=∠2,则弧DE的长为( )| A. | 1π | B. | 1.5π | C. | 2π | D. | 3π |
6.在一次献爱心的捐赠活动中,某班45名同学捐款金额统计如下:
在这次活动中,该班同学捐款金额的众数和中位数分别是50,50.
| 金额(元) | 20 | 30 | 35 | 50 | 100 |
| 学生数(人) | 5 | 10 | 5 | 15 | 10 |
13.掷一枚质地均匀的硬币10次,则下列说法正确的是( )
| A. | 掷2次必有1次正面朝上 | B. | 必有5次正面朝上 | ||
| C. | 可能有5次正面朝上 | D. | 不可能10次正面朝上 |
11.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |