题目内容
8.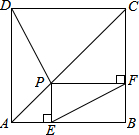 如图,在正方形ABCD中,点P是对角线AC上一点,过点P分别作AB、BC的垂线,垂足为E、F,连接EF.求证:PD=EF.
如图,在正方形ABCD中,点P是对角线AC上一点,过点P分别作AB、BC的垂线,垂足为E、F,连接EF.求证:PD=EF.
分析 可先证明△ABP≌△ADP,再证明四边形PEBF为矩形,由矩形的性质可证得PD=EF.
解答 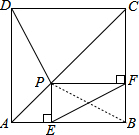 证明:连接BP,如图,
证明:连接BP,如图,
∵四边形ABCD是正方形,
∴AB=AD,∠BAC=∠DAC,∠ABC=90°,
在△ABP和△ADP中
$\left\{\begin{array}{l}{AB=AD}\\{∠DAC=∠BAC}\\{AP=AP}\end{array}\right.$
∴△ABP≌△ADP(SAS),
∴BP=PD,
∵PE⊥AB,PF⊥BC,
∴∠PEB=∠PFB=∠ABC=90°,
∴四这形PEBF为矩形,
∴BP=EF,
∴PD=EF.
点评 本题主要考查正方形的性质及全等三角形的判定和性质,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS、和HL.

练习册系列答案
相关题目
16.某市移动公司为了调查手机发送短信息的情况,在本区域的120位用户中抽取了10位用户来统计他们某周发信息的条数,结果如下表:
本次调查中这120位用户大约每周一共发送2400条短信息.
| 手机用户序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 发送短信息条数 | 20 | 19 | 20 | 20 | 21 | 17 | 15 | 23 | 20 | 25 |
3.把直线y=-x+l沿y轴向上平移一个单位,得到新直线的关系式是( )
| A. | y=-x | B. | y=-x+2 | C. | y=-x-2 | D. | y=-2x |
18.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是方程2x+ay=5的解,则a的值是( )
| A. | a=1 | B. | a=3 | C. | a=-2 | D. | a=-3 |
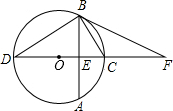 如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.
如图,⊙O的直径CD垂直于弦AB,垂足为E,F为DC延长线上一点,且∠CBF=∠CDB.