题目内容
20.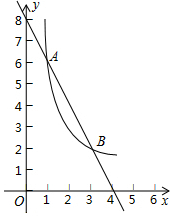 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.(1)求这两个函数的表达式;
(2)根据图象直接写出kx+b-$\frac{m}{x}$<0的x的取值范围.
分析 (1)把A(1,6)代入反比例函数表达式,进而求得B点坐标,由A,B坐标和待定系数法可求得一次函数的解析式;
(2)观察图形,一次函数的值小于反比例函数的值,即在第一象限内,一次函数在反比例函数下面的部分.
解答 解:(1)∵把A(1,6),代入反比例函数表达式中,
m=1×6=6,
∴反比例函数表达式为:y=$\frac{6}{x}$,
把B(3,n)代入得
n=2.
∴B(3,2),
把A(1,6),B(3,2)代入一次函数表达式,得
$\left\{\begin{array}{l}{6=k+b}\\{2=3k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-2}\\{b=8}\end{array}\right.$,
∴一次函数表达式为:y=-2x+8;
(2)有图象可知0<x<1或x>3.
点评 此题考查了反比例函数与一次函数的交点问题,待定系数法求函数解析式,根据图象比较函数值大小,注意掌握待定系数法的应用是关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
8.交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征.其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:
(1)根据上表信息,下列三个函数关系式中,刻画q,v关系最准确的是③(只填上正确答案的序号)
①q=90v+100;②q=$\frac{32000}{v}$;③q=-2v2+120v.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:
| 速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
| 流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
①q=90v+100;②q=$\frac{32000}{v}$;③q=-2v2+120v.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
10.下列运算正确的是( )
| A. | 3m-2m=1 | B. | (m3)2=m6 | C. | (-2m)3=-2m3 | D. | m2+m2=m4 |
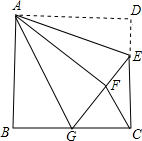 如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.
如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是①②③④⑤.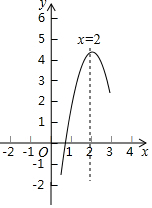 如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)
如图,是二次函数y=ax2+bx-c的部分图象,由图象可知关于x的一元二次方程ax2+bx=c的两个根可能是x1=0.8,x2=3.2合理即可.(精确到0.1)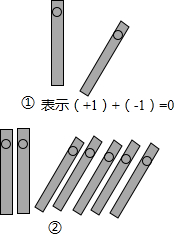 中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.
中国人最先使用负数,魏晋时期的数学家刘徽在“正负术”的注文中指出,可将算筹(小棍形状的记数工具)正放表示正数,斜放表示负数.如图,根据刘徽的这种表示法,观察图①,可推算图②中所得的数值为-3.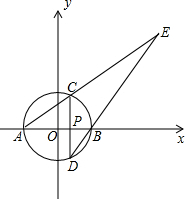 如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.
如图,以原点O为圆心,3为半径的圆与x轴分别交于A,B两点(点B在点A的右边),P是半径OB上一点,过P且垂直于AB的直线与⊙O分别交于C,D两点(点C在点D的上方),直线AC,DB交于点E.若AC:CE=1:2.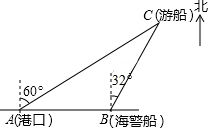 (7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】
(7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】