题目内容
9.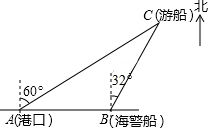 (7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】
(7分)一艘游船从港口A处以北偏东60°的方向出港观光.航行170海里至C处时发生了事故.船长立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东32°方向.若海警船以60海里/时的速度前往救援,求海警船到达事故船C处大约所需的时间.(精确到0.1小时)【参考数据:sin32°=0.53,cos32°=0.85.tan32°=0.62】
分析 过点C作CD⊥AB交AB延长线于D.先解Rt△ACD得出CD=$\frac{1}{2}$AC=85海里,再解Rt△CBD中,得出BC=$\frac{CD}{cos∠BCD}$=$\frac{85}{cos32°}$海里,然后根据时间=路程÷速度即可求出海警船到大事故船C处所需的时间.
解答 解:如图,过点C作CD⊥AB交AB延长线于D.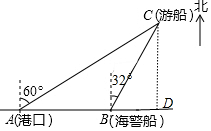
在Rt△ACD中,∵∠ADC=90°,∠CAD=30°,AC=80海里,
∴CD=$\frac{1}{2}$AC=85海里.
在Rt△CBD中,∵∠CDB=90°,∠BCD=32°,
∴BC═$\frac{CD}{cos∠BCD}$=$\frac{85}{cos32°}$ 海 海里,
∴海警船到大事故船C处所需的时间大约为:$\frac{85}{cos32°}$÷60=$\frac{85}{0.85}$÷60≈1.7(小时).
答:海警船到大事故船C处所需的大约时间为1.7小时.
点评 本题考查了解直角三角形的应用-方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.将不等式4x-3<1的解集表示在数轴上,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
18.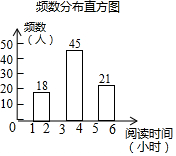 在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
(1)填空:a=30,b=150,m=0.2,n=0.24;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
 在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:频率分布表
| 阅读时间 (小时) | 频数 (人) | 频率 |
| 1≤x<2 | 18 | 0.12 |
| 2≤x<3 | a | m |
| 3≤x<4 | 45 | 0.3 |
| 4≤x<5 | 36 | n |
| 5≤x<6 | 21 | 0.14 |
| 合计 | b | 1 |
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
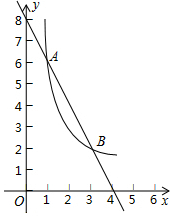 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
 小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上.
小明想要测量学校食堂和食堂正前方一棵树的高度,他从食堂楼底M处出发,向前走3米到达A处,测得树顶端E的仰角为30°,他又继续走下台阶到达C处,测得树的顶端E的仰角是60°,再继续向前走到大树底D处,测得食堂楼顶N的仰角为45°.已知A点离地面的高度AB=2米,∠BCA=30°,且B、C、D三点在同一直线上. 设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题:
设a、b是任意两个实数,用max{a,b}表示a、b两数中较大者,例如:max{-1,-1}=-1,max{1,2}=2,max{4,3}=4,参照上面的材料,解答下列问题: