题目内容
8.交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征.其中流量q(辆/小时)指单位时间内通过道路指定断面的车辆数;速度v(千米/小时)指通过道路指定断面的车辆速度;密度k(辆/千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量q与速度v之间关系的部分数据如下表:
| 速度v(千米/小时) | … | 5 | 10 | 20 | 32 | 40 | 48 | … |
| 流量q(辆/小时) | … | 550 | 1000 | 1600 | 1792 | 1600 | 1152 | … |
①q=90v+100;②q=$\frac{32000}{v}$;③q=-2v2+120v.
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知q,v,k满足q=vk,请结合(1)中选取的函数关系式继续解决下列问题.
①市交通运行监控平台显示,当12≤v<18时道路出现轻度拥堵.试分析当车流密度k在什么范围时,该路段将出现轻度拥堵;
②在理想状态下,假设前后两车车头之间的距离d(米)均相等,求流量q最大时d的值.
分析 (1)利用函数的增减性即可判断;
(2)利用配方法,根据二次函数的性质即可解决问题;
(3)①求出v=12或18时,定义的k的值即可解决问题;
②由题意流量q最大时d的值=流量q最大时k的值;
解答 解:(1)函数①q=90v+100,q随v的增大而增大,显然不符合题意.
函数②q=$\frac{32000}{v}$q随v的增大而减小,显然不符合题意.
故刻画q,v关系最准确的是③.
故答案为③.
(2)∵q=-2v2+120v=-2(v-30)2+1800,
∵-2<0,
∴v=30时,q达到最大值,q的最大值为1800.
(3)①当v=12时,q=1152,此时k=96,
当v=18时,q=1512,此时k=84,
∴84<k≤96.
②当v=30时,q=1800,此时k=60,
∵在理想状态下,假设前后两车车头之间的距离d(米)均相等,
∴流量q最大时d的值为$\frac{1000}{60}$=$\frac{50}{3}$m.
点评 本题考查二次函数的应用、最值问题等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.将不等式4x-3<1的解集表示在数轴上,正确的是( )
| A. |  | B. |  | C. |  | D. |  |
18.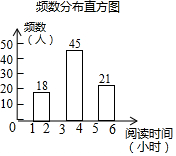 在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
频率分布表
(1)填空:a=30,b=150,m=0.2,n=0.24;
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
 在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:
在开展“经典阅读”活动中,某学校为了解全校学生利用课外时间阅读的情况,学校团委随机抽取若干名学生,调查他们一周的课外阅读时间,并根据调查结果绘制了如下尚不完整的统计表.根据图表信息,解答下列问题:频率分布表
| 阅读时间 (小时) | 频数 (人) | 频率 |
| 1≤x<2 | 18 | 0.12 |
| 2≤x<3 | a | m |
| 3≤x<4 | 45 | 0.3 |
| 4≤x<5 | 36 | n |
| 5≤x<6 | 21 | 0.14 |
| 合计 | b | 1 |
(2)将频数分布直方图补充完整(画图后请标注相应的频数);
(3)若该校由3000名学生,请根据上述调查结果,估算该校学生一周的课外阅读时间不足三小时的人数.
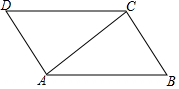 如图,AC是平行四边形ABCD的对角线.
如图,AC是平行四边形ABCD的对角线.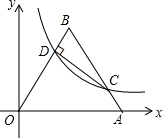 如图,正三角形△OAB的边OA在x轴上,D是OB边上的动点(不与端点O,B重合),双曲线y=$\frac{k}{x}$过点D,且与BA交于点C,设AB=8,$\frac{BD}{BO}$=n.
如图,正三角形△OAB的边OA在x轴上,D是OB边上的动点(不与端点O,B重合),双曲线y=$\frac{k}{x}$过点D,且与BA交于点C,设AB=8,$\frac{BD}{BO}$=n.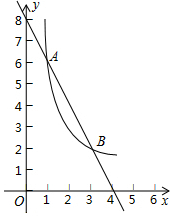 如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.
如图,一次函数y=kx+b(k≠0)与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限内交于A(1,6),B(3,n)两点.