题目内容
10.第五届男篮亚洲杯将2014年7月11-19日在武汉举行.为了抓住商机,某商店决定购进A、B两种纪念品.若购进A种纪念品10件,B种纪念品5件,需要1000元;若购进A种纪念品5件,B种纪念品3件,需要550元.(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定拿出1万元全部用来购进这两种纪念品,考虑到市场需求,要求购进A种纪念品的数量多于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在第(2)问的各种进货方案中,总利润W元能否超过3900元?请说明理由.
分析 (1)关系式为:A种纪念品10件需要钱数+B种纪念品5件钱数=1000;A种纪念品5件需要钱数+B种纪念品3件需要钱数=550;
(2)关系式为:A种纪念品需要的钱数+B种纪念品需要的钱数≤10000;购进A种纪念品的数量不少于B种纪念品数量的6倍,且不超过B种纪念品数量的8倍;
(3)计算出各种方案的利润,比较即可.
解答 解:(1)设A,B两种纪念品每件需x元,y元.
$\left\{\begin{array}{l}{10x+5y=1000}\\{5x+3y=550}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=50}\\{y=100}\end{array}\right.$.
答:A,B两种纪念品每件需50元,100元;
(2)设购买A种纪念品a件,B种纪念品b件.
$\left\{\begin{array}{l}{50a+100b=10000}\\{6b≤a≤8b}\end{array}\right.$,
解得20≤b≤25.
则b=20,21,22,23,24,25;
对应的a=160,158,156,154,152,150
答:商店共有6种进货方案.
(3)解:设利润为W元,则W=20a+30b=20(200-2b)+30b=-10b+4000(20≤b≤25),
∴W随着b的增大而减小,
∴当b=20时,W最大,此时a=160时,W最大,
∴W最大=4000-10×20=3800(元),
答:方案获利最大为:A种纪念品160件,B种纪念品20件,最大利润为3800元.
点评 本题考查了二元一次方程组的应用和一元一次不等式的应用.解决本题的关键是读懂题意,找到符合题意的相应的关系式是解决问题的关键,注意第二问应求得整数解.

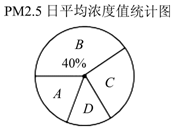 环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5[1]检测,某日随机抽取25个监测点的数据,并绘制成统计表和扇形统计图如下:
环境检测中心在京津冀、长三角、珠三角等城市群以及直辖市和省会城市进行PM2.5[1]检测,某日随机抽取25个监测点的数据,并绘制成统计表和扇形统计图如下:| 类别 | 组别 | PM2.5日平均浓度值 (微克/立方米) | 频数 | 百分比 |
| A | 1 | 15≤浓度值<30 | 2 | 8% |
| 2 | 30≤浓度值<45 | 3 | 12% | |
| B | 3 | 45≤浓度值<60 | a | b |
| 4 | 60≤浓度值<75 | 5 | 20% | |
| C | 5 | 75≤浓度值<90 | 6 | c |
| D | 6 | 90≤浓度值<105 | 4 | 16% |
| 合计 | 25 | 1.00 | ||
根据图表中提供的信息解答下列问题:
(1)统计表中的a=5,b=20%,c=24%;
(2)在扇形统计图中,A类所对应的圆心角是72度;
(3)我国PM2.5安全值的标准采用世卫组织(WHO)设定的最宽限值:日平均浓度小于75微克/立方米.请你估计当日环保监测中心在检测100个城市中,PM2.5日平均浓度值符合安全值的城市约有多少个?
| A. | k=1 | B. | k=2 | C. | k=-1 | D. | k=-2 |
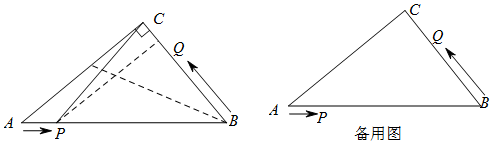
 如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为3$\sqrt{3}$.
如图,菱形ABCD中,AB=6,∠A=120°,点M、N、P分别为线段AB、AD、BD上的任意一点,则PM+PN的最小值为3$\sqrt{3}$.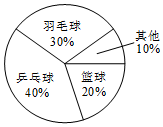 某校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢篮球的人数比最喜欢乒乓球的人数少8人,则该校被调查的学生总人数为40名.
某校在“你最喜爱的球类运动”调查中,随机调查了若干名学生(每名学生分别选了一项球类运动),并根据调查结果绘制了如图所示的扇形统计图.已知其中最喜欢篮球的人数比最喜欢乒乓球的人数少8人,则该校被调查的学生总人数为40名.