题目内容
19.如图,在Rt△ABC中,∠C=90°,AB=10cm,AC=8cm.点P从点A出发沿AB方向向点B运动,速度为1cm/s,同时点Q从点B出发沿B→C→A方向向点A运动,速度为2cm/s.当一个动点到达终点时,另一个动点也随之停止运动.设运动时间为t(s).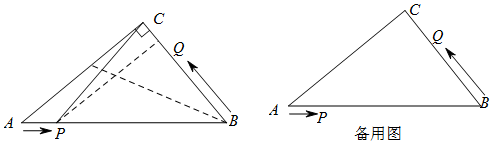
(1)当t为何值时,△APC为等腰三角形.
(2)当点Q在线段BC上运动时,△PBQ的面积为S(cm2),写出S与t之间的函数关系.
(3)当点Q在线段BC上运动时,是否存在某一时刻t,使S△PBQ:S四边形APQC=5:3?若存在,求出t值;若不存在,说明理由.
(4)在运动过程中,是否存在某一时刻t,使BQ平分∠ABC?若存在,求出t的值;若不存在,请说明理由.
分析 (1)分两种情形讨论求解①当AP=PB时,可以证明PA=PC.②当AC=AP时;
(2)当点Q在边BC上运动时,过点Q作QH⊥AB于H,由△QHB∽△ACB,推出$\frac{QH}{AC}$=$\frac{QB}{AB}$,可得QH=$\frac{8}{5}$xcm,根据y=$\frac{1}{2}$BP•QH,列出式子即可;
(3)存在.如图作QH⊥AB于H.由S△PBQ:S四边形APQC=5:3,可得-$\frac{4}{5}$x2+8x=$\frac{5}{8}$×$\frac{1}{2}$×6×8,解方程即可解决问题;
(4)存在.如图作QH⊥AB于H.首先证明QC=QH=2t-6,由△AQH∽△ABC,可得$\frac{AQ}{AB}$=$\frac{QH}{BC}$,推出$\frac{14-2t}{10}$=$\frac{2t-6}{6}$,解方程即可解决问题;
解答 解:(1)①当AP=PB时,∵∠ACB=90°,
∴CP=PA=PB,
∴t=5,
②当AC=AP时,t=8,
∴t=5s或8s时,△APC是等腰三角形.
(2)当点Q在边BC上运动时,过点Q作QH⊥AB于H,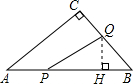
∵AP=xcm,
∴BP=(10-x)cm,BQ=2xcm,
∵△QHB∽△ACB,
∴$\frac{QH}{AC}$=$\frac{QB}{AB}$,
∴QH=$\frac{8}{5}$xcm,
y=$\frac{1}{2}$BP•QH=$\frac{1}{2}$(10-x)•$\frac{8}{5}$x=-$\frac{4}{5}$x2+8x(0<x≤3).
(3)存在.∵S△PBQ:S四边形APQC=5:3,
∴-$\frac{4}{5}$x2+8x=$\frac{5}{8}$×$\frac{1}{2}$×6×8,
解得x=$\frac{15}{2}$或$\frac{5}{2}$,
∴t=$\frac{15}{2}$s或$\frac{5}{2}$s时,S△PBQ:S四边形APQC=5:3.
(4)存在.如图作QH⊥AB于H.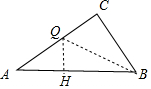
∵∠QBC=∠QBA,QC⊥BC,QH⊥AB,
∴QC=QH=2t-6,AQ=14-2t,
∵∠A=∠A,∠AHQ=∠C=90°,
∴△AQH∽△ABC,
∴$\frac{AQ}{AB}$=$\frac{QH}{BC}$,
∴$\frac{14-2t}{10}$=$\frac{2t-6}{6}$,
∴t=$\frac{9}{2}$,
∴t=$\frac{9}{2}$s时,BQ平分∠ABC.
点评 本题考查四边形综合题、定义是矩形的判定和性质、相似三角形的判定和性质等知识,解题的关键是学会利用参数构建方程解决问题,学会添加常用辅助线,构造直角三角形解决问题,属于中考压轴题.

 Rt△ABC中,∠ACB=90°,直线DE过C点,且有DE∥AB,若∠1=65°,则∠2的度数是( )
Rt△ABC中,∠ACB=90°,直线DE过C点,且有DE∥AB,若∠1=65°,则∠2的度数是( )| A. | 25° | B. | 35° | C. | 50° | D. | 65° |
 ,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .
,将△ABC 绕点 C 逆时针旋转 60°,得到△MNC, 连接 BM,则 BM 的长是 .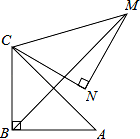
 ,
, 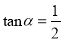 ,求四边形OBEC的面积。
,求四边形OBEC的面积。