题目内容
 如图,AB⊥DC,GF⊥AB,D、F为垂足.G在BC上,∠1=∠2.请判断DE与BC的位置关系并说明理由.
如图,AB⊥DC,GF⊥AB,D、F为垂足.G在BC上,∠1=∠2.请判断DE与BC的位置关系并说明理由.考点:平行线的判定与性质
专题:几何图形问题
分析:先根据垂直的定义得∠BFG=∠BDC=90°,则根据平行线的判定方法得CD∥GF,再根据平行线的性质得∠2=∠GCD,由于∠1=∠2,根据等量代换得∠GCD=∠1,于是根据平行线的判定得DE∥BC.
解答:解:DE∥BC.理由如下:
∵AB⊥DC,GF⊥AB,
∴∠BFG=∠BDC=90°,
∴CD∥GF,
∴∠2=∠GCD,
∵∠1=∠2,
∴∠GCD=∠1,
∴DE∥BC.
∵AB⊥DC,GF⊥AB,
∴∠BFG=∠BDC=90°,
∴CD∥GF,
∴∠2=∠GCD,
∵∠1=∠2,
∴∠GCD=∠1,
∴DE∥BC.
点评:本题考查了平行线的判定与性质:同位角相等,两直线平行,内错角相等,两直线平行;两直线平行,同位角相等.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
在四边形ABCD中,若AB∥CD,添上以下条件能使四边形ABCD是平行四边形的是( )
①∠A=∠C;②AD∥BC;③AD=BC;④AB=CD.
①∠A=∠C;②AD∥BC;③AD=BC;④AB=CD.
| A、①②③ | B、①②④ |
| C、②③④ | D、②④ |
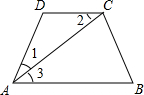 如图,AC平分∠DAB,∠1=∠2,求证:AB∥CD.
如图,AC平分∠DAB,∠1=∠2,求证:AB∥CD.