题目内容
12.若函数y=(k-2)${x}^{{k}^{2}-5}$是反比例函数,则k=-2.在每个象限内,y随x的增大而增大.分析 根据反比例函数的定义列出方程$\left\{\begin{array}{l}{{k}^{2}-5=-1}\\{k-2≠0}\end{array}\right.$,解出k的值,并判断y随x的变化趋势即可.
解答 解:若函数y=(k-2)xk2-5是反比例函数,则$\left\{\begin{array}{l}{{k}^{2}-5=-1}\\{k-2≠0}\end{array}\right.$,
解得k=-2,
∵k=-2<0,
∴在每个象限内,y随x的增大而增大.
故答案为:-2,增大.
点评 本题考查反比例函数的定义,熟记反比例函数解析式的一般式 y=$\frac{k}{x}$(k≠0)是解决此类问题的关键.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
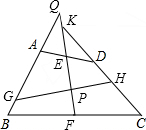 如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.
如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.