题目内容
12.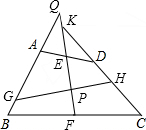 如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.
如图,四边形ABCD中,AB=CD,点E,F分别是AD,BC的中点,GH⊥EF交于点P.延长BA,FE相交于点Q,延长CD交FE的延长线于点K,求证:∠AGH=∠DHG.
分析 如图,连接BD,作BD的中点M,连接EM、FM.利用三角形中位线定理证得△MEF是等腰三角形,则∠EMP=∠FMP.利用三角形中位线定理、平行线的性质推知∠AGH=∠EMP,∠DHG=∠FMP根据等量代换证得∠AGH=∠DHG.
解答 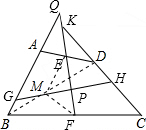 证明:如图,连接BD,作BD的中点M,连接EM、FM,
证明:如图,连接BD,作BD的中点M,连接EM、FM,
∵点E是AD的中点,
∴ME是△ADG的中位线,
∴ME∥AB,ME=$\frac{1}{2}$AB,
∴∠AGH=∠EMP,
同理可证:MF∥DC,MF=$\frac{1}{2}$DC,
∴∠DHG=∠FMP,
∵AB=CD,
∴ME=MF,
∵GH⊥EF,
∴∠EMP=∠FMP,
∴∠AGH=∠DHG.
点评 本题考查了三角形的中位线平行于第三边并且等于第三边的一半,平行线的性质,等腰三角形的判定与性质,熟记各性质与定理并作辅助线构造出三角形是解题的关键.

练习册系列答案
相关题目
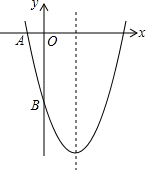 如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).
如图,已知二次函数y=ax2-4x+c的图象与坐标轴交于点A(-1,0)和点B(0,-5).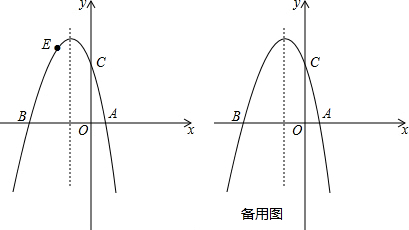
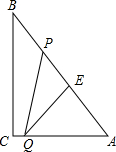 如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm.当点Q到达顶点C时,P,Q同时停止运动.设P,Q两点运动时间为t秒.
如图,Rt△ABC中,∠C=90°,BC=8cm,AC=6cm.点P从B出发沿BA 向A运动,速度为每秒1cm,点E是点B以P为对称中心的对称点.点P运动的同时,点Q从A出发沿AC向C运动,速度为每秒2cm.当点Q到达顶点C时,P,Q同时停止运动.设P,Q两点运动时间为t秒. 在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE.
在平行四边形ABCD中,如果点E是CD的中点,点F是BC边上的一点,且∠FAE=∠EAD,求证:EF⊥AE. 已知方程组$\left\{\begin{array}{l}{ax-3y=5}\\{2x-by=1}\end{array}\right.$所对应的图象如图所示,试求出3a+7b的值.
已知方程组$\left\{\begin{array}{l}{ax-3y=5}\\{2x-by=1}\end{array}\right.$所对应的图象如图所示,试求出3a+7b的值.