��Ŀ����
����������10�֣���1�����ⷢ��
��ͼ1����ACB�͡�DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ��١�AEB�Ķ���Ϊ ��
���߶�AD��BE֮���������ϵ�� ��
��2����չ̽��
��ͼ2����ACB�͡�DCE��Ϊ����ֱ�������Σ���ACB=��DCE=900�� ��A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����жϡ�AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�


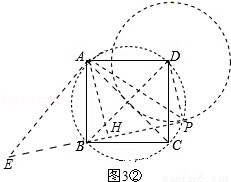
��3�����������ͼ3����������ABCD�У�CD= ������P����PD=1���ҡ�BPD=900����ֱ��д����A��BP�ľ��룮
������P����PD=1���ҡ�BPD=900����ֱ��д����A��BP�ľ��룮

��1����60����AD=BE����2����AEB��900��AE=2CM+BE�����ɼ������������3��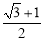 ��
�� ��
��
��������
�����������1����������֤��ACD�ա�BCE���Ӷ��õ���AD=BE����ADC=��BEC���ɵ�A��D��E��ͬһֱ���Ͽ������ADC���Ӷ����������AEB�Ķ�����
��2�����գ�1���еĽⷨ�������AEB�Ķ�����֤��AD=BE���ɡ�DCEΪ����ֱ�������μ�CMΪ��DCE��DE���ϵĸ߿ɵ�CM=DM=ME���Ӷ�֤��AE=2CH+BE��
��3����PD=1�ɵã���P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ��ɡ�BPD=90��ɵã���P����BDΪֱ����Բ�ϣ���Ȼ����P��������Բ�Ľ��㣬������Բ���������㣬�������������λ�÷ֱ�������ۣ�Ȼ�������ʵ��ĸ����ߣ������ڣ�2���еĽ��ۼ��ɽ�����⣮
�����������1������ͼ1��
�ߡ�ACB�͡�DCE��Ϊ�ȱ������Σ���CA=CB��CD=CE����ACB=��DCE=60�㣮���ACD=��BCE��
�ڡ�ACD�͡�BCE�У���AC=BC����ACD=��BCE��CD=CE��
���ACD�ա�BCE��SAS�������ADC=��BEC��
�ߡ�DCEΪ�ȱ������Σ����CDE=��CED=60�㣮
�ߵ�A��D��E��ͬһֱ���ϣ����ADC=120�㣬���BEC=120�㣬���AEB=��BEC����CED=60�㣮
�ʴ�Ϊ��60�㣮
�ڡߡ�ACD�ա�BCE����AD=BE���ʴ�Ϊ��AD=BE��
��2����AEB=90�㣬AE=BE+2CM��
���ɣ���ͼ2��
�ߡ�ACB�͡�DCE��Ϊ����ֱ�������Σ���CA=CB��CD=CE����ACB=��DCE=90�㣬���ACD=��BCE��
�ڡ�ACD�͡�BCE�У���CA=CB����ACD=��BCE��CD=CE�����ACD�ա�BCE��SAS����
��AD=BE����ADC=��BEC��
�ߡ�DCEΪ����ֱ�������Σ����CDE=��CED=45�㣮
�ߵ�A��D��E��ͬһֱ���ϣ����ADC=135�㣬���BEC=135�㣬���AEB=��BEC����CED=90�㣮
��CD=CE��CM��DE����DM=ME��
�ߡ�DCE=90�㣬��DM=ME=CM����AE=AD+DE=BE+2CM��
��3����PD=1�����P���Ե�DΪԲ�ģ�1Ϊ�뾶��Բ�ϣ�
�ߡ�BPD=90�㣬���P����BDΪֱ����Բ�ϣ����P������Բ�Ľ��㣮
�ٵ���P����ͼ3����ʾλ��ʱ��
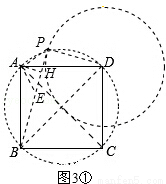
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����BP�ڵ�E����ͼ3�٣�
���ı���ABCD�������Σ����ADB=45�㣮AB=AD=DC=BC=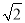 ����BAD=90�㣬��BD=2��
����BAD=90�㣬��BD=2��
��DP=1����BP=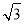 ��
��
��A��P��D��B�ĵ㹲Բ�����APB=��ADB=45�㣬���PAE�ǵ���ֱ�������Σ�
�֡ߡ�BAD�ǵ���ֱ�������Σ���B��E��P���ߣ�AH��BP�����ɣ�2���еĽ��ۿɵã�BP=2AH+PD��
��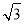 =2AH+1����AH=
=2AH+1����AH=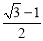 ��
��
�ڵ���P����ͼ3����ʾλ��ʱ��
����PD��PB��PA����AH��BP������ΪH��
����A��AE��AP����PB���ӳ����ڵ�E����ͼ3�ڣ�
ͬ���ɵã�BP=2AH��PD����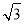 =2AH��1����AH=
=2AH��1����AH=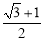 ��
��
������������A��BP�ľ���Ϊ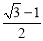 ��
��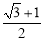 ��
��
���㣺1��Բ���ۺ��⣻2��ȫ�������ε��ж������ʣ�3�������ε����ʣ�4��Բ�ܽǶ�����





 ����
���� ��n B��
��n B��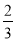
 ����
����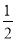 ��n
��n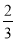 ����
���� ��n��1 D��
��n��1 D��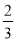
 ����
���� ��n��
��n�� =
= ��DE��4����BC��ֵΪ�� ��
��DE��4����BC��ֵΪ�� ��
 ������a��b��c�ֱ�Ϊ��ABC���ߵij���
������a��b��c�ֱ�Ϊ��ABC���ߵij��� �Ƿ��̵ĸ������жϡ�ABC����״����˵�����ɣ�
�Ƿ��̵ĸ������жϡ�ABC����״����˵�����ɣ�
 ��������ABCD����������ABCD��x�����������������x���Ϲ���������A�����λص�x ����ʱ����A�˶���·����x��Χ�ɵ�ͼ�ε������Ϊ ���� ��
��������ABCD����������ABCD��x�����������������x���Ϲ���������A�����λص�x ����ʱ����A�˶���·����x��Χ�ɵ�ͼ�ε������Ϊ ���� ��
 B��
B�� C��
C�� D��
D��