Question

（本题满分12分）如图，在矩形ABCD中，AB=3，BC=4．动点P从点A出发沿AC向终点C运动，同时动点Q从点B出发沿BA向点A运动，到达A点后立刻以原来的速度沿AB返回．点P，Q运动速度均为每秒1个单位长度，当点P到达点C时停止运动，点Q也同时停止．连结PQ，设运动时间为t（t >0）秒．

（1）当点Q从B点向A点运动时（未到达A点），若△APQ ∽△ABC，求t的值；

（2）伴随着P，Q两点的运动，线段PQ的垂直平分线为直线l．

①当直线l经过点A时，射线QP交AD边于点E，求AE的长；

②是否存在t的值，使得直线l经过点B？若存在，请求出所有t的值；若不存在，请说明理由．

 

 

Answer 1

（1）；（2）①AE=3；②存在，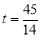

【解析】

试题分析：（1）∵△APQ∽△ABC ∴， 即 解得 3分

（2）①如图①，线段PQ的垂直平分线为l经过点A，则AP=AQ，

即3－t=t，∴t=1.5，∴AP=AQ=1.5，

过点Q作QO∥AD交AC于点O，

则∴，

，∴PO=AO－AP=1．

由△APE∽△OPQ，得． 6分

②（ⅰ）如图②，当点Q从B向A运动时l经过点B，

BQ＝BP＝AP＝t，∠QBP＝∠QAP

∵∠QBP＋∠PBC＝90°，∠QAP＋∠PCB＝90°

∴∠PBC＝∠PCB CP＝BP＝AP＝t

∴CP＝AP＝AC＝×5＝2.5∴t＝2.5 9分

（ⅱ）如图③，当点Q从A向B运动时l经过点B，

BP＝BQ＝3－（t－3）＝6－t，AP＝t，PC＝5－t，

过点P作PG⊥CB于点G，由△PGC∽△ABC，

得

，BG＝4－=

由勾股定理得，即

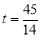，解得． 12分

考点: 矩形的综合运用