题目内容
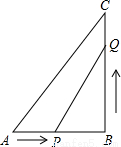
如图,已知在Rt△ABC中,AB=AC=2,在△ABC内作第一个内接正方形DEFG;然后取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形依次进行下去,则第n个内接正方形的边长为( )

A. ·(
·( )n B.
)n B.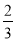
 ·(
·(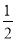 )n
)n
C.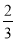 ·(
·( )n-1 D.
)n-1 D.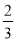
 ·(
·( )n-
)n-
D
【解析】
试题分析:∵在Rt△ABC中,AB=AC=2,
∴∠B=∠C=45°,BC= =2
=2 ,
,
∵在△ABC内作第一个内接正方形DEFG;
∴EF=EC=DG=BD,
∴DE= BC,
BC,
∴DE= ,
,
∵取GF的中点P,连接PD、PE,在△PDE内作第二个内接正方形HIKJ;再取线段KJ的中点Q,在△QHI内作第三个内接正方形依次进行下去,
∴ =
= =
= ,
,
∴EI= KI=
KI= HI,
HI,
∵DH=EI,
∴HI= DE=(
DE=( )2﹣1×
)2﹣1× ,
,
则第n个内接正方形的边长为: ×(
×( )n﹣1.
)n﹣1.
故选:D.

考点: 1.相似三角形的判定与性质;2.正方形的性质

练习册系列答案
相关题目
 有最高点,则m=___________
有最高点,则m=___________ =
= ,CF⊥AB于点F,CE⊥AD的延长线于点E.
,CF⊥AB于点F,CE⊥AD的延长线于点E.




 .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
 是方程
是方程 的两个实数根,
的两个实数根,
 的值为( )
的值为( )
 ∽
∽ ,相似比为1:2,且保证
,相似比为1:2,且保证 的坐标为( , );
的坐标为( , ); ),那么它的对应点
),那么它的对应点 的坐标为( , ).
的坐标为( , ).