题目内容
16.如果一个三角形三边的长分别为1,$\sqrt{2}$,$\sqrt{3}$,那么这个三角形最长边上的高与中线夹角的正切值为$\frac{\sqrt{2}}{4}$.分析 根据三角形三边的长分别为1,$\sqrt{2}$,$\sqrt{3}$,由勾股定理的逆定理可得该三角形为直角三角形,然后根据等积法可以求得斜边上的高,根据直角三角形斜边上的中线等于斜边的一半,可以求出斜边中线的长度,从而可以推导出该三角形最长边上的高与中线夹角的正切值.
解答 解:∵三角形三边的长分别为1,$\sqrt{2}$,$\sqrt{3}$,
又∵${1}^{2}+(\sqrt{2})^{2}=(\sqrt{3})^{2}$,
∴该三角形为直角三角形.
如下图所示:令BC=1,AC=$\sqrt{2}$,AB=$\sqrt{3}$,CD⊥AB,CE为斜边AB上的中线,
则$\frac{CD×AB}{2}=\frac{AC×BC}{2}$,CE=$\frac{AB}{2}=\frac{\sqrt{3}}{2}$,
解得,CD=$\frac{\sqrt{6}}{3}$.
∵CD⊥AB,CE=$\frac{AB}{2}=\frac{\sqrt{3}}{2}$,CD=$\frac{\sqrt{6}}{3}$,
∴DE=$\sqrt{C{E}^{2}-C{D}^{2}}$=$\frac{\sqrt{3}}{6}$,
∴tan∠ECD=$\frac{DE}{CD}=\frac{\frac{\sqrt{3}}{6}}{\frac{\sqrt{6}}{3}}=\frac{\sqrt{2}}{4}$,
故答案为$\frac{\sqrt{2}}{4}$.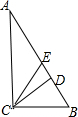
点评 本题考查勾股定理的逆定理,解直接三角函数,直角三角形斜边上的中线和斜边的关系,根据直角三角形三条边可以求出斜边上的高,本题的关键是理清题意,正确作答.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目

 如图,要在一个形状为圆的纸板上截出一个面积最大的正方形,试用尺规作出这个正方形(不要求写作法,保留作图痕迹)
如图,要在一个形状为圆的纸板上截出一个面积最大的正方形,试用尺规作出这个正方形(不要求写作法,保留作图痕迹)
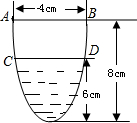 一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是2$\sqrt{3}$cm.
一个横断面是抛物线的渡槽如图所示,根据图中所给的数据求出水面的宽度是2$\sqrt{3}$cm.