题目内容
15.如图,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.(1)猜想图1中线段BG、线段DE的长度关系及所在直线的位置关系.
(2)将图1中的正方形CEFG绕着点C旋转一定的角度,得到如图2的情形.请你通过观察、测量等方法判断(1)中得到的结论是否仍然成立?说明理由.

分析 (1)由正方形的性质得出BC=CD,CE=CG,∠BCD=∠ECG=90°,由SAS证明△BCG≌△DCE,得出BG=DE,∠CBG=∠CDE,延长BG交DE于H,由角的互余关系和对顶角相等证出∠CDE+∠DGH=90°,由三角形内角和定理得出∠DHG=90°即可;
(2)由正方形的性质可得BC=CD,CE=CG,∠BCD=∠ECG=90°,然后求出∠BCG=∠DCE,由SAS证明△BCG和△DCE全等,由全等三角形对应边相等可得BG=DE,全等三角形对应角相等可得∠CBG=∠CDE,然后求出∠DOH=90°,再根据垂直的定义证明即可.
解答 (1)解:BG=DE,BG⊥DE;理由如下:
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=DC}&{\;}\\{∠BCG=∠ECG}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
延长BG交DE于H,如图所示: ∵∠CBG+∠BGC=90°,∠DGH=∠BGC,
∵∠CBG+∠BGC=90°,∠DGH=∠BGC,
∴∠CDE+∠DGH=90°,
∴∠DHG=90°,
∴BG⊥DE;
(2)解:成立;理由如下:
∵四边形ABCD是正方形,四边形CEFG是正方形,
∴BC=CD,CE=CG,∠BCD=∠ECG=90°,
∴∠BCD+∠DCG=∠ECG+∠DCG,
即∠BCG=∠DCE,
在△BCG和△DCE中,
$\left\{\begin{array}{l}{BC=CD}&{\;}\\{∠BCG=∠DCE}&{\;}\\{CG=CE}&{\;}\end{array}\right.$,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
∵∠CBG+∠BHC=90°,∠BHC=∠DHO(对顶角相等),
∴∠CDE+∠DHO=90°,
在△DHO中,∠DOH=180°-(∠CDE+∠DHO)=180°-90°=90°,
∴BG⊥DE.
点评 本题考查了正方形的性质、全等三角形的判定与性质、对顶角相等、三角形内角和定理;熟记性质并准确识图确定出三角形全等的条件是解题的关键,也是本题的难点.

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案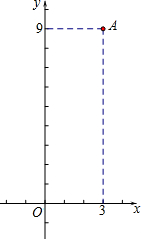 某校初三数学社团成员一起研究二次函数.他们发现一个二次函数的图象具有以下性质:①它是一个轴对称图形,②图象经过原点,③在y轴左侧,y随x的增大而减小,在y轴的右侧,y随x的增大而增大,④经过点A(3,9)
某校初三数学社团成员一起研究二次函数.他们发现一个二次函数的图象具有以下性质:①它是一个轴对称图形,②图象经过原点,③在y轴左侧,y随x的增大而减小,在y轴的右侧,y随x的增大而增大,④经过点A(3,9)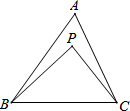 如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=80°,那么∠BPC=105°.
如图,BP与CP相交于点P,∠ABP=$\frac{1}{4}$∠ABC,∠ACP=$\frac{1}{4}$∠ACB,∠A=80°,那么∠BPC=105°.