题目内容
5.已知,抛物线y=ax2+bx+3满足2a+b=0,写出该抛物线上可以确定的点的坐标(0,3)(2,3).分析 由题意得到y=ax2+bx+3=ax2-2ax+a-a+3=ax(x-2)+3,即可求得抛物线y=ax2+bx+3一定经过点(2,3),
求得对称轴x=-$\frac{-2a}{a}$=2,然后根据抛物线的对称性即可求得对称点坐标.
解答 解:∵抛物线y=ax2+bx+3满足2a+b=0,
∴b=-2a,
∴y=ax2+bx+3=ax2-2ax+a-a+3=ax(x-2)+3,
∴抛物线y=ax2+bx+3一定经过点(2,3),
∵对称轴x=-$\frac{-2a}{a}$=2,
∴点(2,3)的对称点为(0,3),
∴抛物线y=ax2+bx+3一定经过点(0,3),
故答案为(0,3)(2,3).
点评 本题主要考查对二次函数图象上点的坐标特征的理解和掌握,能根据已知得出过(2,3)和对称轴是解此题的关键.

练习册系列答案
 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
16.如果设5a=m,5b=n,那么5a-b等于( )
| A. | m+n | B. | mn | C. | m-n | D. | $\frac{m}{n}$ |
13.下列实数中,是无理数的为( )
| A. | -3.567 | B. | 0.101001 | C. | $\sqrt{2}$ | D. | $\frac{1}{3}$ |
15.计算正确的是( )
| A. | (a+b)2=a2+b2 | B. | x2+x3=x5 | C. | (ab2)3=a2b5 | D. | 2a2•a-1=2a |
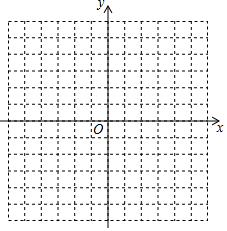 (1)在如图所示的平面直角坐标系中表示下面各点:
(1)在如图所示的平面直角坐标系中表示下面各点: