题目内容
2.已知:A=2a2+2ab-2a-1,B=-a2+ab-1(1)求A-(A-2B)的值;
(2)若A+2B的值与a的取值无关,求b的值.
分析 (1)先去括号,再把B=-a2+ab-1代入即可;
(2)先求出A+2B的表达式,再根据其值与a的取值无关,求出b的值即可、
解答 解:(1)A-(A-2B)=A-A+2B=2B
∵B=-a2+ab-1,
∴原式=2B
=2(-a2+ab-1)
=-2a2+2ab-2;
(2)∵A=2a2+2ab-2a-1,B=-a2+ab-1,
∴A+2B=2a2+2ab-2a-1+2(-a2+ab-1)
=2a2+2ab-2a-1-2a2+2ab-2
=4ab-2a-3.
∵A+2B的值与a的取值无关,
∴4ab-2a-3与a的取值无关,即(4b-2)a-3与a的取值无关
∴4b-2=0,解得b=$\frac{1}{2}$.
答:b的值为$\frac{1}{2}$.
点评 本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.

练习册系列答案
相关题目
12.如果a、b、c是一个直角三角形的三边,则a:b:c可以等于( )
| A. | 2:2:4 | B. | 3:4:5 | C. | 3:5:7 | D. | 1:3:9 |
11.树的高度与树生长的年数有关,测得某棵树的有关数据如下表(树苗原高80厘米):
(1)填出第4年树苗可能达到的高度;
(2)请用含a的代数式表示:a年后树的高度h=7a+80;
(3)根据这种长势,12年后这棵树可能达到的高度是164厘米.
| 年数a | 高度h(单位:厘米) |
| 1 | 87 |
| 2 | 94 |
| 3 | 101 |
| 4 | 108 |
| … | … |
(2)请用含a的代数式表示:a年后树的高度h=7a+80;
(3)根据这种长势,12年后这棵树可能达到的高度是164厘米.
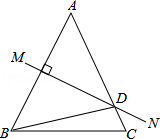 如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是50度.
如图,等腰△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,∠DBC=15°,则∠A的度数是50度. 如图,DE是△ABC中AC边上的垂直平分线,若BC=9,AB=11,则△EBC的周长为20.
如图,DE是△ABC中AC边上的垂直平分线,若BC=9,AB=11,则△EBC的周长为20.