题目内容
13.已知二次函数y=ax2-2x+c的图象经过点A(-2,0)、B(3,0)(1)求二次函数的解析式;
(2)求这抛物线的对称轴和顶点坐标;
(3)试画出这抛物线的大致图象.
分析 (1)分别将点A和点B的坐标代入函数解析式,然后即可得出a和c的值;
(2)把求得的函数解析式化成顶点式即可得出顶点P的坐标.
(3)利用描点法画二次函数图象.
解答 解:(1)∵二次函数y=ax2-2x+c的图象经过点A(-2,0)、B(3,0),
∴$\left\{\begin{array}{l}{4a+4+c=0}\\{9a-6+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=2}\\{c=-12}\end{array}\right.$
∴二次函数的解析式为y=2x2-2x-12;
(2)∵二次函数的解析式为y=2x2-2x-12=2(x-$\frac{1}{2}$)2-$\frac{25}{2}$,
∴对称轴为x=$\frac{1}{2}$,顶点P的坐标为($\frac{1}{2}$,-$\frac{25}{2}$).
(3)画出函数的图象如图: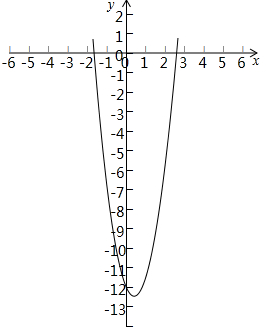
点评 此题考查了待定系数法求二次函数解析式的知识及二次函数的顶点坐标的知识,属于基础题,解答本题的关键是待定系数法的运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.方程(x+4)(x-5)=0的根是( )
| A. | x=-4 | B. | x1=4,x2=-5 | C. | x=5 | D. | x1=-4,x2=5 |
18.定义一种新运算“?”,规定:a?b=$\frac{1}{3}$a-4b,则12?(-1)=( )
| A. | 0 | B. | -8 | C. | 8 | D. | 6 |
 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=40°,则∠BOD=100°.
如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=40°,则∠BOD=100°. 如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E
如图,在矩形ABCD中,点F在边BC上,且AF=AD,过点D作DE⊥AF,垂足为点E 如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°
如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°