题目内容
12.观察如图各正方形图案,每条边上有n(n≥2)个圆点,每个图案中圆点的总数是s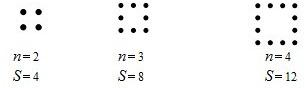
按此规律推断出:n=20,s=76.
分析 由图可知:当n=2时,圆点的总个数为:S=2×4-4=4;当n=3时,圆点的总个数为:S=3×4-4=8;当n=4时,圆点的总个数为:S=4×4-4=12;…由此得出当n=n时,图形中圆点的总个数为:S=4n-4;进一步代入计算得出答案即可.
解答 解:∵当n=2时,圆点的总个数为:S=2×4-4=4;
当n=3时,圆点的总个数为:S=3×4-4=8;
当n=4时,圆点的总个数为:S=4×4-4=12;
…
∴当n=n时,圆点的总个数为:S=4n-4;
∴当n=20时,圆点的总个数为:S=4×20-4=76.
故答案为:76.
点评 此题考查图形的变化规律,找出图形之间的联系,得出运算规律解决问题.

练习册系列答案
相关题目
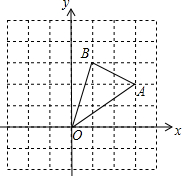 如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°
如图,在边长为1的正方形组成网格中,△AOB的顶点均在格点上,点A、B的坐标分别是A(3,2)、B(1,3),将△AOB绕点O逆时针旋转90°
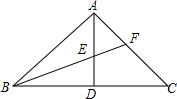 如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,BF平分∠ABC,交AD于E,交于AC于F.求证:$\frac{DE}{AE}=\frac{AF}{CF}$.