题目内容
 如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,若△ODP是腰长为5的等腰三角形,则满足条件的点P有
如图,在平面直角坐标系中,O为原点,四边形OABC是矩形,A(10,0),C(0,3),点D是OA的中点,点P在BC边上运动,若△ODP是腰长为5的等腰三角形,则满足条件的点P有考点:矩形的性质,坐标与图形性质,等腰三角形的判定,勾股定理的应用
专题:分类讨论
分析:分为三种情况①OP=OD=5,②DP=OD=5,③OP=DP=5,根据勾股定理求出CP,OM即可.
解答: 解:过P作PM⊥OA于M.
解:过P作PM⊥OA于M.
①当OP=OD时,
OP=5,CO=3,
∴易得CP=4,
∴P(4,3);
②当OD=PD时,
PD=DO=5,PM=3,
∴易得MD=4,从而CP=1或CP'=9,
∴P(1,3)或(9,3);
综上,满足题意的点P的坐标为(4,3)、(1,3)、(9,3),
综上所述,符合题意的点P有3个.
故答案是:3.
 解:过P作PM⊥OA于M.
解:过P作PM⊥OA于M.①当OP=OD时,
OP=5,CO=3,
∴易得CP=4,
∴P(4,3);
②当OD=PD时,
PD=DO=5,PM=3,

∴易得MD=4,从而CP=1或CP'=9,
∴P(1,3)或(9,3);
综上,满足题意的点P的坐标为(4,3)、(1,3)、(9,3),
综上所述,符合题意的点P有3个.
故答案是:3.
点评:本题考查了矩形性质,等腰三角形的判定,坐标与图形性质,勾股定理的应用,关键是求出符合条件的所有情况.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
在芦山地震抢险时,某镇部分村庄需8组战士步行运送物资,要求每组分配的人数相同,若按每组人数比预定人数多分配1人,则总数会超过100人;若按每组人数比预定人数少分配1人,则总数不足90人.设预定每组分配的人数是x,则x应满足的不等式组是( )
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
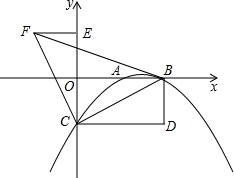 如图,抛物线y=-
如图,抛物线y=- 如图,平面直角坐标系内,AC=BC,M为AC上一点,BM平分△ABC的周长,若AB=6,S△BMC=3.6,则点A的坐标为
如图,平面直角坐标系内,AC=BC,M为AC上一点,BM平分△ABC的周长,若AB=6,S△BMC=3.6,则点A的坐标为