Question

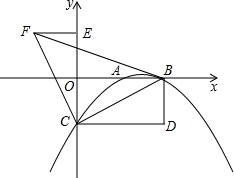如图，抛物线y=-

1

4

x²+

3

2

x-2交x轴于A，B两点（点A在点B的左侧），交y轴于点C，分别过点B，C作y轴，x轴的平行线，两平行线交于点D，将△BDC绕点C逆时针旋转，使点D旋转到y轴上得到△FEC，连接BF．
（1）求点B，C所在直线的函数解析式；
（2）求△BCF的面积；
（3）在线段BC上是否存在点P，使得以点P，A，B为顶点的三角形与△BOC相似？若存在，求出点P的坐标；若不存在，请说明理由．

Answer 1

考点：二次函数综合题,三角形的面积,勾股定理,旋转的性质,相似三角形的应用

专题：压轴题,分类讨论

分析：（1）根据坐标轴上点的坐标特征可得点B，C的坐标，再根据待定系数法可得点B，C所在直线的函数解析式；
（2）根据勾股定理可得BC的长，根据旋转的性质和三角形面积公式即可求解；
（3）存在．分两种情况讨论：①过A作AP₁⊥x轴交线段BC于点P₁，则△BAP₁∽△BOC；②过A作AP₂⊥BC，垂足点P₂，过点P₂作P₂Q⊥x轴于点Q．则△BAP₂∽△BCO；依此讨论即可求解．

解答：解：（1）当y=0时，-

1

4

x²+

3

2

x-2=0，
解得x₁=2，x₂=4，
∴点A，B的坐标分别为（2，0），（4，0），
当x=0时，y=-2，
∴C点的坐标分别为（0，-2），
设直线BC的解析式为y=kx+b（k≠0），
则

b=-2 4k+b=0

，
解得

k= 1 2 b=-2

．
∴直线BC的解析式为y=

1

2

x-2；

（2）∵CD∥x轴，BD∥y轴，
∴∠ECD=90°，
∵点B，C的坐标分别为（4，0），（0，-2），
∴BC=

OB2+OC2

=

42+22

=2

5

，
∵△FEC是由△BDC绕点C逆时针旋转得到，
∴△BCF的面积=

1

2

BC•FC=

1

2

×2

5

×2

5

=10；

（3）存在．
分两种情况讨论：
①过A作AP₁⊥x轴交线段BC于点P₁，则△BAP₁∽△BOC，
∵点A的坐标为（2，0），
∴点P₁的横坐标是2，
∵点P₁在点BC所在直线上，
∴y=

1

2

x-2=

1

2

×2-2=-1，
∴点P₁的坐标为（2，-1）；
②过A作AP₂⊥BC，垂足点P₂，过点P₂作P₂Q⊥x轴于点Q．
∴△BAP₂∽△BCO，
∴

AP2

CO

=

AB

CB

，

AP2

CO

=

BP2

OB

∴

AP2

2

=

2

2 5

，
解得AP₂=

2 5

5

，
∵

AP2

CO

=

BP2

OB

，
∴AP₂•BP=CO•BP₂，
∴

2 5

5

×4=2BP₂，
解得BP₂=

4 5

5

，
∵

1

2

AB•QP₂=

1

2

AP₂•BP₂，
∴2QP₂=

2 5

5

×

4 5

5

，
解得QP₂=

4

5

，
∴点P₂的纵坐标是-

4

5

，
∵点P₂在BC所在直线上，
∴x=

12

5

∴点P₂的坐标为（

12

5

，-

4

5

），
∴满足条件的P点坐标为（2，-1）或（

12

5

，-

4

5

）．

点评：考查了二次函数综合题，涉及的知识点为：坐标轴上点的坐标特征，待定系数法可求直线的函数解析式，勾股定理可，旋转的性质，三角形面积，分类思想，相似三角形的性质，综合性较强，有一定的难度．