题目内容
14. 如图,长方形OABC的边OA长为1,边AB长为$\sqrt{3}$,OC在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点左边于一点D,则点D表示的实数是-2.
如图,长方形OABC的边OA长为1,边AB长为$\sqrt{3}$,OC在数轴上,以原点O为圆心,对角线OB的长为半径画弧,交数轴上原点左边于一点D,则点D表示的实数是-2.
分析 根据勾股定理计算出OB长度,根据弧的性质知OB=OD.进而求出答案.
解答 解:∵长方形OABC的边OA长为1,边AB长为$\sqrt{3}$,
∴OB=$\sqrt{3+1}$=2,
∵OB=OD,
∴OD=2,
∵O为原点,点D在原点左侧,
∴点D表示的实数是-2.
故答案为:-2.
点评 题目考查了实数与数轴,通过勾股定理为桥梁,计算数轴上点所表示的数.题目整体较为简单,适合随堂训练.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
5.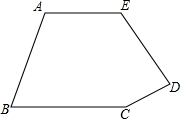 如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )
如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )
 如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )
如图,在五边形ABCDE中,∠CDE=80°,为了保证AE∥BC,则∠BCD+∠AED应等于( )| A. | 100° | B. | 260° | C. | 280° | D. | 275° |
6. 如图的几何体的俯视图是( )
如图的几何体的俯视图是( )
 如图的几何体的俯视图是( )
如图的几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |
3.将下列长度的三根木棒首尾顺次连接,能组成三角形的是( )
| A. | 1,2,4 | B. | 8,6,4 | C. | 12,6,5 | D. | 3,3,6 |
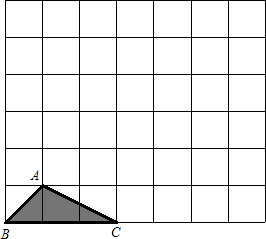 按要求完成作图.
按要求完成作图.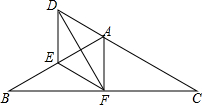 如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.
如图,△ABC中,AB=AC=6,F为BC的中点,D为CA延长线上一点,∠DFE=∠B.