题目内容
14.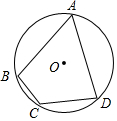 如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )
如图,已知⊙O为四边形ABCD的外接圆,O为圆心,若∠BCD=120°,AB=AD=2,则⊙O的半径长为( )| A. | $\frac{3\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
分析 连接BD,作OE⊥AD,连接OD,先由圆内接四边形的性质求出∠BAD的度数,再由AD=AB可得出△ABD是等边三角形,则DE=$\frac{1}{2}$AD,∠ODE=$\frac{1}{2}$∠ADB=30°,根据锐角三角函数的定义即可得出结论.
解答  解:连接BD,作OE⊥AD,连接OD,
解:连接BD,作OE⊥AD,连接OD,
∵⊙O为四边形ABCD的外接圆,∠BCD=120°,
∴∠BAD=60°.
∵AD=AB=2,
∴△ABD是等边三角形.
∴DE=$\frac{1}{2}$AD=1,∠ODE=$\frac{1}{2}$∠ADB=30°,
∴OD=$\frac{DE}{cos30°}$=$\frac{2\sqrt{3}}{3}$.
故选D.
点评 本题考查的是圆内接四边形的性质,熟知圆内接四边形对角互补是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
5.若抛物线y=x2-4x+2-t(t为实数)在0<x<$\frac{5}{2}$的范围内与x轴有公共点,则t的取值范围为( )
| A. | -2<t<2 | B. | -2≤t<2 | C. | -$\frac{7}{4}$<t<2 | D. | t≥-2 |
2.株洲市展览馆某天四个时间段进出馆人数统计如下,则馆内人数变化最大时间段为( )
| 9:00-10:00 | 10:00-11:00 | 14:00-15:00 | 15:00-16:00 | |
| 进馆人数 | 50 | 24 | 55 | 32 |
| 出馆人数 | 30 | 65 | 28 | 45 |
| A. | 9:00-10:00 | B. | 10:00-11:00 | C. | 14:00-15:00 | D. | 15:00-16:00 |
4. 如图,梯形ABCD中,AB∥CD,∠D=( )
如图,梯形ABCD中,AB∥CD,∠D=( )
 如图,梯形ABCD中,AB∥CD,∠D=( )
如图,梯形ABCD中,AB∥CD,∠D=( )| A. | 120° | B. | 135° | C. | 145° | D. | 155° |
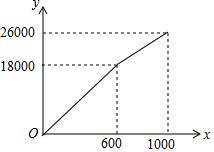 为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).
为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为x(m2),种草所需费用y1(元)与x(m2)的函数关系式为${y}_{1}=\left\{\begin{array}{l}{{k}_{1}x(0≤x<600)}\\{{k}_{2}x+b(600≤x≤1000)}\end{array}\right.$,其图象如图所示:栽花所需费用y2(元)与x(m2)的函数关系式为y2=-0.01x2-20x+30000(0≤x≤1000).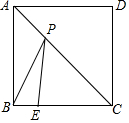 如图所示,正方形ABCD的边长为4,E是边BC上的一点,且BE=1,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是6.
如图所示,正方形ABCD的边长为4,E是边BC上的一点,且BE=1,P是对角线AC上的一动点,连接PB、PE,当点P在AC上运动时,△PBE周长的最小值是6.