题目内容
已知方程x2-4x+2-k2=0,且k≠0,不解方程证明:
(1)方程有两个不相等的实数根;
(2)方程有一根大于1,另一根小于1.
(1)方程有两个不相等的实数根;
(2)方程有一根大于1,另一根小于1.
考点:抛物线与x轴的交点
专题:证明题
分析:(1)判断上述方程的根的情况,只要看根的判别式△=b2-4ac的值的符号就可以了.
(2)利用根与系数的关系以及(x1-1)(x2-1)=x1x2-(x1+x2)+1,确定两个根的取值情况.
(2)利用根与系数的关系以及(x1-1)(x2-1)=x1x2-(x1+x2)+1,确定两个根的取值情况.
解答:证明:(1)∵有两个不相等的实数根,a=1,b=-4,c=2-k2,
∴△=b2-4ac=(-4)2-4×1×(2-k2)=8+4k2>0,
∴方程两个不相等的实数根
(2)设方程有两个根为x1和x2,
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=2-k2-4+1=-k2-1,
∵k为实数且k≠0,
∴-k2<0,
∴-k2-1<0,
因此方程的一个根>1,另一个根<1.
∴△=b2-4ac=(-4)2-4×1×(2-k2)=8+4k2>0,
∴方程两个不相等的实数根
(2)设方程有两个根为x1和x2,
∴(x1-1)(x2-1)=x1x2-(x1+x2)+1=2-k2-4+1=-k2-1,
∵k为实数且k≠0,
∴-k2<0,
∴-k2-1<0,
因此方程的一个根>1,另一个根<1.
点评:本题考查了抛物线和x轴的交点问题,判断一元二次方程根的情况与判别式△的关系,可以转化为判断方程的根的判别式与0的大小关系,另外本题根据方程的一个根>1,另一个根<1,转化为(x1-1)(x2-1)<0,是解题的关键.

练习册系列答案
相关题目
下列等式正确的是( )
A、3
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
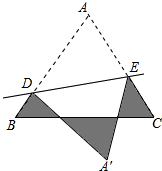 如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )
如图,等边三角形ABC的边长为1cm,DE分别是AB、AC上的点,将△ABC沿直线DE折叠,点A落在点A′处,且点A′在△ABC外部,则阴影部分的周长为( )| A、2cm | B、2.5cm |
| C、3cm | D、3.5cm |

 如图,在平面直角坐标系中,过点C(0,4)的直线l1与过点O的直线l2交于点B(2
如图,在平面直角坐标系中,过点C(0,4)的直线l1与过点O的直线l2交于点B(2 如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,求证:①△ADE≌△CBF;②∠A=∠C.
如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,求证:①△ADE≌△CBF;②∠A=∠C. 如图,已知:在?ABCD中,AC为对角线,DE交AC于F,交AB于E,AE:EB=1:2,S△AEF=5,求S△CDF的值.
如图,已知:在?ABCD中,AC为对角线,DE交AC于F,交AB于E,AE:EB=1:2,S△AEF=5,求S△CDF的值.