题目内容
 如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,求证:①△ADE≌△CBF;②∠A=∠C.
如图,已知AB=CD,AD=CB,E、F分别是AB,CD的中点,且DE=BF,求证:①△ADE≌△CBF;②∠A=∠C.考点:全等三角形的判定与性质
专题:证明题
分析:①求出AE=CF,根据全等三角形的判定定理SSS推出即可;
②根据全等三角形的性质得出即可.
②根据全等三角形的性质得出即可.
解答:证明:①∵E、F分别是AB,CD的中点,
∴AE=
AB,CF=
CD,
∵AB=CD,
∴AE=CF,
在△ADE和△CBF中
∴△ADE≌△CBF(SSS);
②∵△ADE≌△CBF,
∴∠A=∠C.
∴AE=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB=CD,
∴AE=CF,
在△ADE和△CBF中
|
∴△ADE≌△CBF(SSS);
②∵△ADE≌△CBF,
∴∠A=∠C.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

练习册系列答案
相关题目
 如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=4,AB=6,AD=14,在AD上能否找到一点P,使△PAB和△PCD相似?若能,共有几个符合条件的点P?并求相应PD的长.若不能,说明理由.
如图,在直角梯形ABCD中,AB∥CD,DA⊥AB,CD=4,AB=6,AD=14,在AD上能否找到一点P,使△PAB和△PCD相似?若能,共有几个符合条件的点P?并求相应PD的长.若不能,说明理由.一次函数y=kx+b,现分别从装有1,-2两张数字卡片的甲口袋和装有-1,2,3三张数字卡片的乙口袋中随机抽一张,甲口袋的卡片上的数字作k,乙口袋的卡片上的数字作b,则该一次函数的图象经过一、二、四象限的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
如果|a|=3,那么a+1的值是( )
| A、4 | B、-2 |
| C、4或-2 | D、3或-3 |
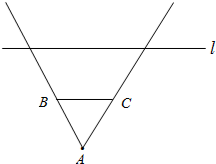 如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为
如图,小明同学站在离墙(BC)5米的A处,发现小强同学在离墙(BC)20米远且与墙平行的一条公路l上骑车,已知墙BC长为24米,小强骑车速度10米/秒,则小明看不见小强的时间为 如图:在等边△ABC内取一点D,使DA=DB,在△ABC外取一点E,使∠DBE=∠DBC,且BE=BA,则∠BED=
如图:在等边△ABC内取一点D,使DA=DB,在△ABC外取一点E,使∠DBE=∠DBC,且BE=BA,则∠BED=