题目内容
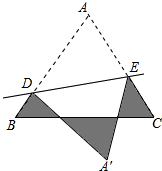如图，等边三角形ABC的边长为1cm，DE分别是AB、AC上的点，将△ABC沿直线DE折叠，点A落在点A′处，且点A′在△ABC外部，则阴影部分的周长为（ ）| A、2cm | B、2.5cm |
| C、3cm | D、3.5cm |
考点：翻折变换（折叠问题）
专题：
分析：由题意得到DA′=DA，EA′=EA，经分析判断得到阴影部分的周长等于△ABC的周长即可解决问题．
解答：
解：如图，由题意得：
DA′=DA，EA′=EA，
∴阴影部分的周长=DA′+EA′+DB+CE+BG+GF+CF
=（DA+BD）+（BG+GF+CF）+（AE+CE）
=AB+BC+AC=1+1+1=3（cm）．
故选C．
解：如图，由题意得：DA′=DA，EA′=EA，
∴阴影部分的周长=DA′+EA′+DB+CE+BG+GF+CF
=（DA+BD）+（BG+GF+CF）+（AE+CE）
=AB+BC+AC=1+1+1=3（cm）．
故选C．
点评：该题主要考查了翻折变换的性质及其应用问题；解题的关键是准确找出该题图形中隐含的等量关系，灵活分析判断，准确计算解答．
练习册系列答案
相关题目
如图，在直角梯形ABCD中，AB∥CD，DA⊥AB，CD=4，AB=6，AD=14，在AD上能否找到一点P，使△PAB和△PCD相似？若能，共有几个符合条件的点P？并求相应PD的长．若不能，说明理由．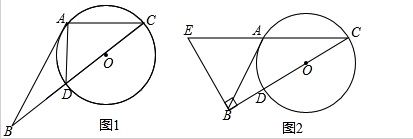
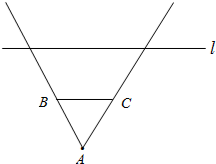如图，小明同学站在离墙（BC）5米的A处，发现小强同学在离墙（BC）20米远且与墙平行的一条公路l上骑车，已知墙BC长为24米，小强骑车速度10米/秒，则小明看不见小强的时间为
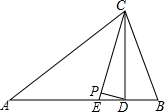在△ABC中，∠A=38°，∠B=70°，CD⊥AB于点D，CE平分∠ACB，DP⊥CE于点P，求∠CDP的度数．