题目内容
在四边形ABCD中，对角线AC与BD相交于E，∠CAB=∠CBD，已知AB=4，AC=6，BC=5，BD=5.5，求DE的长．
考点：相似三角形的判定与性质
专题：
分析：证△CBA∽△CEB，得出
=
，代入求出BE即可．
| AB |
| BE |
| AC |
| BC |
解答：解：∵在△CBE与△CAB中，
∠BCA=∠BCA，
∠CAB=∠CBD，
∴△CBA∽△CEB，
∴
=
，
∴
=
，
BE=
，
∴DE=BD-BE=5.5-
=
．
∠BCA=∠BCA，
∠CAB=∠CBD，
∴△CBA∽△CEB，
∴
| AB |
| BE |
| AC |
| BC |
∴
| 4 |
| BE |
| 6 |
| 5 |
BE=
| 10 |
| 3 |
∴DE=BD-BE=5.5-
| 10 |
| 3 |
| 13 |
| 6 |
点评：本题考查了相似三角形的性质和判定的应用，解此题的关键是求出BE的长，题目比较好，难度适中．
练习册系列答案
名校通行证有效作业系列答案
相关题目
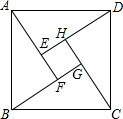四年一度的国际数学家大会于2002年8月20日在北京召开，大会会标如图．它是由四个相同的直角三角形（Rt△AED，Rt△BFA，Rt△CGB，Rt△DHC）与中间的小正方形EFGH拼成的，
如图，AC平分∠BAD，CE⊥AB于E，BC=CD，∠ADC+∠B=180°，探究2AE与AB，AD的数量关系，并加以证明．