Question

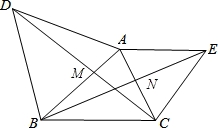
如图，在△ABC中，AB=AC，BE=CD，BD=CF，则∠α与∠A之间的数量关系为__________．

Answer 1

2∠α+∠A=180°．

【考点】全等三角形的判定与性质．

【分析】根据SAS证明△BED与△CDF全等，再利用全等三角形的性质解答即可．

【解答】解：∵AB=AC，

∴∠C=∠B，

在△BED与△CDF中，

，

∴△BED≌△CDF（SAS），

∴∠BED=∠FDC，

∵∠α+∠FDC=∠B+∠BED，

∴∠α=∠B，

∵∠A+∠B+∠C=180°，

∴2∠α+∠A=180°．

故答案为：2∠α+∠A=180°．

【点评】本题考查了全等三角形的判定和性质，三角形外角的性质和三角形内角和定理，熟练掌握性质定理是解题的关键．