Question

如图，△ABD、△AEC都是等边三角形．AB、CD相交于M，AC、BE相交于N，∠MAN=60°．求证：

（1）BE=DC；

（2）AM=AN．

Answer 1

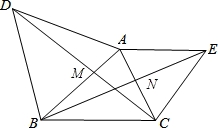
【考点】全等三角形的判定与性质；等边三角形的性质．

【专题】证明题．

【分析】（1）由等边三角形的性质得出AB=AD，AE=AC，∠BAD=∠CAE=60°，证出∠BAE=∠DAC，根据SAS证明△ABE≌△ADC，得出对应边相等即可；

（2）证△ADM≌△ABN即可；

【解答】证明：（1）∵△ABD、△AEC都是等边三角形，

∴AB=AD，AE=AC，∠BAD=∠CAE=60°，

∴∠BAE=∠DAC，

在△ABE和△ADC中，，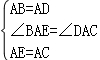

∴△ABE≌△ADC（SAS），

∴BE=DC；

（2）∵△ABE≌△ADC，

∴∠ADM=∠ABN，

在△ADM与△ABN中，

，

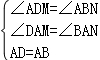∴△ADM≌△ABN（AAS），

∴AM=AN．

【点评】此题主要考查了全等三角形的判定和性质定理、等边三角形的性质，关键是找出或证明能使三角形全等的条件．对于全等三角形的判定定理SAS，ASA，AAS，SSS，HL必须熟练掌握．